

日大工 総合教育 樋口幸治郎
| ホーム | 教室 | 研究室 |
|---|---|---|
| 工科系数学I及び演習 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
これで注意は削がれまい.

--- Leonhard Euler
レオンハルト・オイラーの失明時の言葉
(H. Eves著 Mathematical Circlesより)
冪と対数の定義を学び, これらが満たす重要な法則である指数法則と対数法則を学ぶ. (教科書範囲外)
$a^b$を冪といい, $\log_ac$を対数という. 冪$a^b$や対数$\log_ac$では, $a$を底, $b$を指数, $c$を真数という. つまり, $$冪=底^{指数},\qquad 対数=\log_{底}真数$$
冪は掛け算の繰り返し $$a^n=\overbrace{a\cdot a\cdot\ ......\ \cdot a}^{n個}$$ を基本として, $$a^0=1,\quad a^{-x}=\dfrac{1}{a^x}$$ により, 指数が整数のときの冪を定義し, さらに, 底aが正の数のときには, $$a^{\dfrac{x}{y}}=\sqrt[y]{a^{x}}=(\sqrt[y]{a})^x$$ により, 指数が有理数のときの冪を定義し, さらに, 指数が無理数$r$のときは, $r$に収束する有理数の列$\{r_n\}$を用いて, $$a^r=\lim_{n\to\infty}a^{r_n}$$ と定義する.
また, $$冪\quad\overset{逆}{\iff}\quad対数$$ $$a^b=c\quad\iff\quad \log_ac=b$$ である. 従って, $$\log_ac=``a^b=cとなるb"$$ が成り立つ. $a^0=1$を対数で考えることで $$\log_a1=0$$ が得られる. また, 冪と対数は逆なので $$a^{\log_ab}=b,\qquad \log_a(a^b)=b$$ が成り立つ.
例
$2^4=2\cdot 2\cdot 2\cdot 2=16$,
$5^3=5\cdot 5\cdot 5=125$,
$7^{-2}=\dfrac{1}{7^2}=\dfrac{1}{49}$,
$27^{\dfrac{1}{3}}=\sqrt[3]{27}=3$
$\log_28=``2^b=8となるb"=3$,
$\log_981=``9^b=81となるb"=2$,
$\log_31=``3^b=1となるb"=0$,
$\log_{10}\dfrac{1}{10}=``10^b=\dfrac{1}{10}となるb"=-1$
冪や対数の計算は次の指数法則や対数法則を使うと簡単になることが多い.
$$a^xa^y=a^{x+y},\qquad (a^x)^y=a^{xy},\qquad a^xb^x=(ab)^x$$
説明 $x,y$が有理数のときのみ考える. $x,y$が有理数ならば, 整数$p,q,r$を用いて, $$x=\dfrac{p}{r},\quad y=\dfrac{q}{r}$$ と(分母を通分した形で)書くことができる. $$a^xa^y=(\sqrt[r]{a})^p(\sqrt[r]{a})^q =\overbrace{\sqrt[r]{a}\cdot\ ......\ \cdot\sqrt[r]{a}}^{p個}\cdot\overbrace{\sqrt[r]{a}\cdot\ ......\ \cdot\sqrt[r]{a}}^{q個} =\overbrace{\sqrt[r]{a}\cdot\ ......\ \cdot\sqrt[r]{a}}^{p+q個} =(\sqrt[r]{a})^{p+q} =a^{\dfrac{p+q}{r}} =a^{x+y}$$ $$(a^x)^y=\left(\sqrt[r]{(\sqrt[r]{a})^p}\right)^q =\overbrace{\sqrt[r]{\overbrace{\sqrt[r]{a}\cdot\ ......\ \cdot\sqrt[r]{a}}^{p個}}\cdot\ ......\ \cdot\sqrt[r]{\overbrace{\sqrt[r]{a}\cdot\ ......\ \cdot\sqrt[r]{a}}^{p個}}}^{q個} =\overbrace{\sqrt[r^2]{a}\cdot\ ......\ \cdot\sqrt[r^2]{a}}^{pq個} =a^{\dfrac{pq}{r^2}} =a^{xy}$$ $$a^xb^x=(\sqrt[r]{a})^p(\sqrt[r]{b})^p =\overbrace{\sqrt[r]{a}\cdot\ ......\ \cdot\sqrt[r]{a}}^{p個}\cdot\overbrace{\sqrt[r]{b}\cdot\ ......\ \cdot\sqrt[r]{b}}^{p個} =\overbrace{\sqrt[r]{ab}\cdot\ ......\ \cdot\sqrt[r]{ab}}^{p個} =(ab)^x$$ となることから, 指数法則が成立する.
注意 底が正の実数でないときには, 指数法則を指数に整数以外が現れる形で用いることはできない. 例えば, 次のような議論は間違いである. $$-1=(-1)^1=(-1)^{2\cdot\dfrac{1}{2}} \underset{間違い}{=}((-1)^2)^{\dfrac{1}{2}} =1^{\dfrac{1}{2}} =\sqrt{1} =1$$ より$-1=1$, 移行して$2=0$, 両辺に$\dfrac{r}{2}$ ($r$は任意の数)をかければ$r=0$となるから, すべての数は$0$に等しい.
$$\log_a xy=\log_a x+\log_a y,\qquad \log_a x^y=y\log_ax,\qquad \log_b x=\dfrac{\log_ax}{\log_ab}\quad (底の変換公式)$$
証明 指数法則を使って証明する. $$a^xa^y=a^{x+y},\qquad (a^x)^y=a^{xy}$$であるが, これらをそれぞれ$\log_az$の$z$に代入し, さらに, $x$に$\log_ax$を代入し, 第1の式のみ$y$には$\log_ay$を代入すれば, $$\log_a(xy)=\log_ax+\log_ay,\qquad \log_a(x^y)=(\log_ax)\cdot y$$ と示すべき公式の最初の二つが得られる. 最後に, 今得られた第2の公式において文字を置き換えて $$\log_ab^x=x\log_ab$$ が成り立つことが分かるが, $x$に$\log_bx$を代入すると $$\log_ax=\log_bx\log_ab$$ が得られる. 両辺を$\log_ab$で割れば第3の公式が得られる.
指数関数と対数関数の特徴を学ぶ. またネピアの数の定義を与え, 自然指数,自然対数の定義を学ぶ. (教科書範囲外)
冪$a^b$/対数$\log_ab$について, 指数/真数を変数$x$とした関数を指数関数$a^x$, 対数関数$\log_ax$という(底$a$は$a>0$, $a\ne 1$なる定数とする).
因みに, 冪において底を変数$x$とした関数を冪関数$x^b$という.
冪と対数は逆なので, $$ \begin{align} 指数関数\quad &\overset{逆}{\iff}\quad 対数関数\\ y=a^x\quad &\iff\quad \log_ay=x \end{align} $$ であり, これらのグラフは直線$y=x$について対称になる.
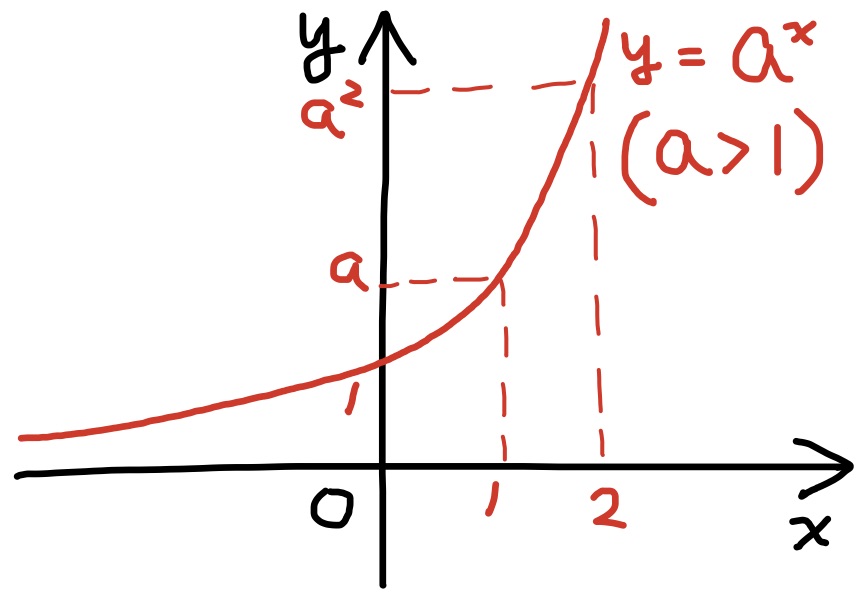
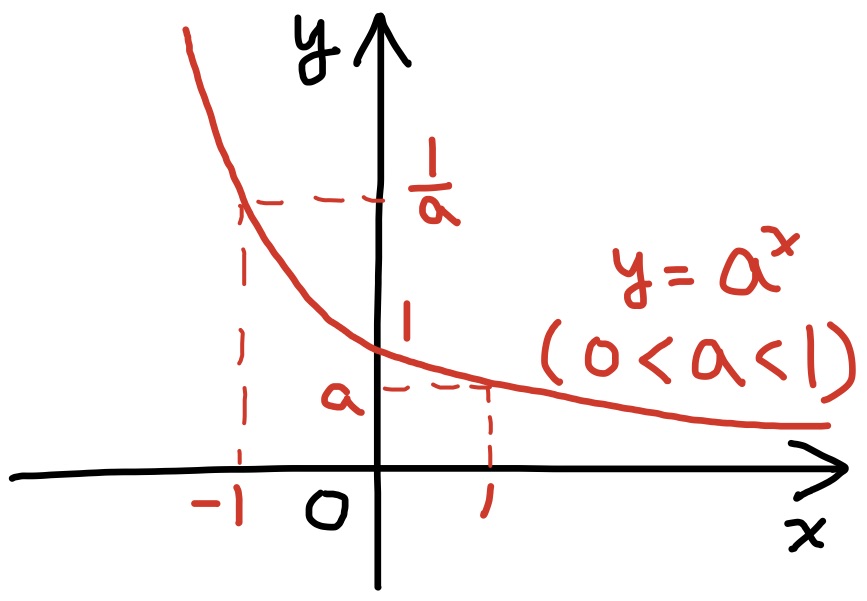
定理 指数関数$a^x$ (但し定数$a$は$a>0, a\ne 1$) は連続な単調関数で, 常に$a^x>0$が成り立つ. また, グラフは下に凸である.
指数関数$a^x$は単調増加で, $\displaystyle\lim_{x\to\infty}a^x=\infty$, $\displaystyle\lim_{x\to-\infty}a^x=0$
指数関数$a^x$は単調減少で, $\displaystyle\lim_{x\to\infty}a^x=0$, $\displaystyle\lim_{x\to-\infty}a^x=\infty$
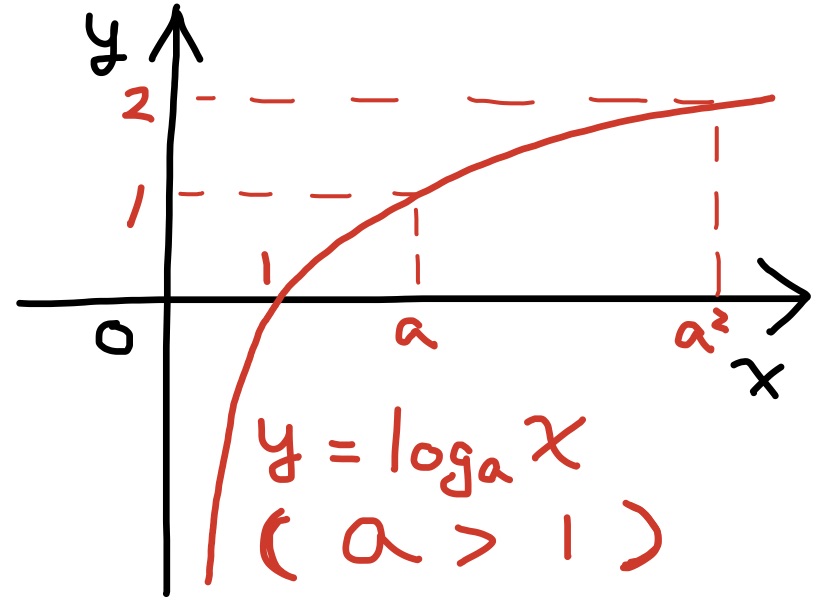
定理 対数関数$\log_ax$ (但し定数$a$は$a>0, a\ne 1$) は正の実数の範囲$(0,\infty)$で定義された連続な単調関数である.
対数関数$\log_ax$は単調増加で, $\displaystyle\lim_{x\to\infty}\log_ax=\infty$, $\displaystyle\lim_{x\searrow 0}\log_ax=-\infty$
対数関数$\log_ax$は単調減少で, $\displaystyle\lim_{x\to\infty}\log_ax=-\infty$, $\displaystyle\lim_{x\searrow 0}\log_ax=\infty$
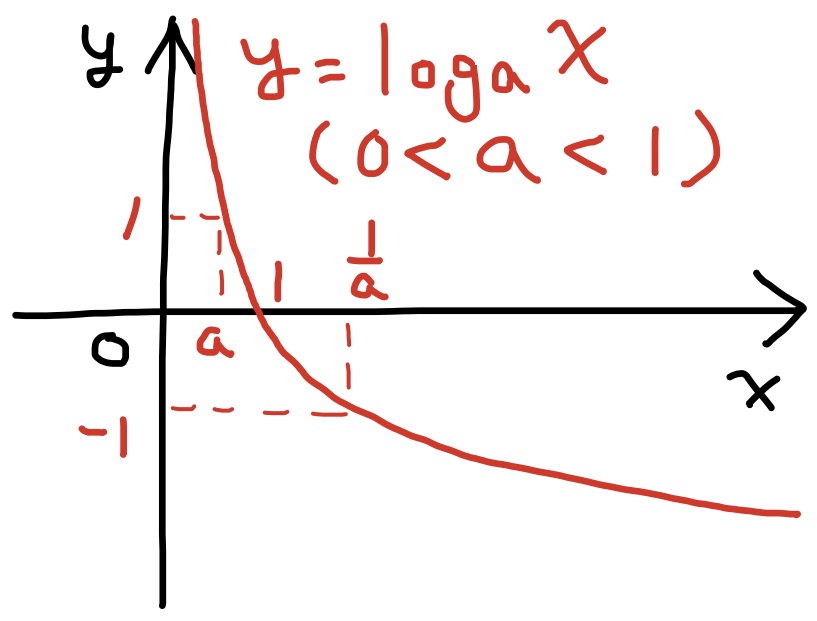
定理 $$\left.(e^x)^\prime\right|_{x=0}=1$$ を満たす正の実数$e$が存在する. この実数$e$をネピアの数といい, また自然な底という.
証明
$f(x)=2^x$の微分可能性を既に示した.
指数関数$f(x)=2^x$は下に凸だから,
$x=0$での平均変化率
$$\dfrac{f(0+h)-f(0)}{h}=\dfrac{2^h-1}{h}$$
は$h$の関数として単調増加である.
従って, $h=-1$のときの平均変化率と$f^\prime(0)$とを比較すれば,
$$\dfrac{2^{-1}-1}{-1}=\dfrac{1}{2}\le f^\prime(0)=\left.(2^x)^\prime\right|_{x=0}$$
であるから,
$f^\prime(0)\ne 0$がわかる.
よって, これの逆数$\dfrac{1}{f^\prime(0)}$を考えることができる.
正の実数$b$について$b=2^{\log_2b}$であるから,
$$\left.(b^x)^\prime\right|_{x=0}
=\left.((2^{\log_2b})^{x})^\prime\right|_{x=0}
=\left.(2^{(\log_2b)x})^\prime\right|_{x=0}
=\left.(2^t)^\prime\right|_{t=0}\cdot((\log_2b)x)^\prime
=\left.(2^x)^\prime\right|_{x=0}\cdot\log_2b$$
$\log_2b$は$b$についての関数として, 連続関数で
$$\lim_{b\to\infty}\log_2b=\infty,\qquad\lim_{b\searrow 0}\log_2b=-\infty$$
であるから,
中間値の定理より$\log_2e=\dfrac{1}{\left.(2^x)^\prime\right|_{x=0}}$
を満たす正の実数$e$が存在する.
上の等式において$b=e$を代入すれば,
$$\left.(e^x)^\prime\right|_{x=0}
=\left.(2^x)^\prime\right|_{x=0}\cdot\log_2e
=1$$
が得られる.
ネピアの数$e$の近似値は $$e \fallingdotseq 2.718281828...$$ であり, $e$は無理数であることが知られている.
定義 ネピアの数$e$を底とした指数関数$e^x$と対数関数$\log_ex$を 自然指数(関数), 自然対数(関数)という. 自然対数$\log_ex$を単に $$\log x$$ と書く. また単に「指数関数」と言って「自然指数」を意味することもある.