定理 $\displaystyle f(x)\le g(x)\quad\Longrightarrow\quad\lim_{x\to a}f(x)\le\lim_{x\to a}g(x)$
注意 定理において左の条件は$x=a$の十分近くで成立すれば良い.
証明 背理法で示す. $\displaystyle\lim_{x\to a}f(x)>\lim_{x\to a}g(x)$という仮定が不合理であることを示せば良い. $$\lim_{x\to a}f(x)>r>\lim_{x\to a}g(x)\tag{1}$$ を満たす$r$を選べば, 極限の意味から $x$が$a$に十分近ければ, $f(x)$は$\lim_{x\to a}f(x)$に, また, $g(x)$は$\lim_{x\to a}g(x)$に十分近いので, 不等式(1)より $$f(x)>r>g(x)$$ が成立するはずだが, これは$f(x)\le g(x)$という定理の条件に矛盾する.
系(はさみ打ちの原理) $f(x)\le g(x)\le h(x)$かつ $\displaystyle\lim_{x\to a}f(x),\lim_{x\to a}h(x)=\alpha\quad\Longrightarrow\quad\lim_{x\to a}g(x)=\alpha$
注意 定理において左の条件の不等式は$x=a$の十分近くで成立すれば良い.
証明 先の定理から, $f(x)\le g(x)\le h(x)$なので, $$\lim_{x\to a}f(x)\le\lim_{x\to a}g(x)\le\lim_{x\to a}h(x)$$ であるが, 最左辺, 最右辺は$\alpha$に等しいので, $$\lim_{x\to a}g(x)=\alpha$$ が成り立つ.
定理 $0< x<\dfrac{\pi}{2}$のとき, $$\cos x< \dfrac{\sin x}{x}< 1$$ が成り立つ.
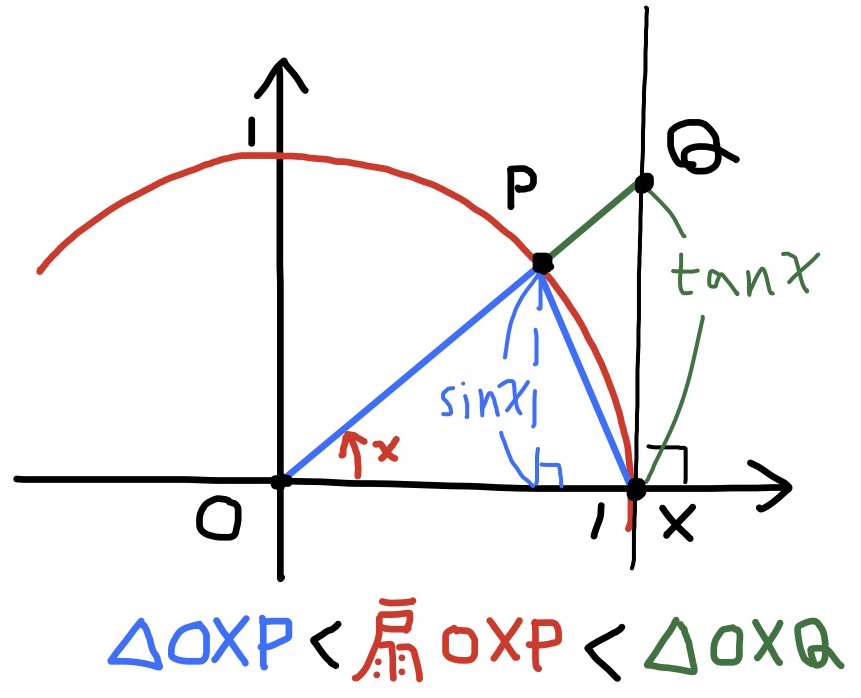
証明 図のように単位円周上で角度$0$,$x$の点をX,Pとし, OPを延長して, Xを通る垂線との交点をQとする. 面積の比較により, $$\triangle{\rm OXP}<{\rm 扇OXP}<\triangle{\rm OXQ}$$ であるから, $\dfrac{1}{2}\cdot 1\cdot \sin x<\dfrac{1}{2}\cdot x\cdot 1^2<\dfrac{1}{2}\cdot 1\cdot\dfrac{\sin x}{\cos x}$ が成り立つ. これから $$\sin x< x< \dfrac{\sin x}{\cos x}$$ が分かる. 左の不等式から$\dfrac{\sin x}{x}<1$が得られ, 右の不等式から$\cos x<\dfrac{\sin x}{x}$が得られるので, 定理の不等式が成立する.
系 $0< x<\dfrac{\pi}{2}$, または, $-\dfrac{\pi}{2}<x<0$のとき, $$\cos x< \dfrac{\sin x}{x}< 1$$ が成り立つ. 従って, 挟み撃ちの原理より $$\lim_{x\to 0}\dfrac{\sin x}{x}=1$$ が成立する.
証明
$0>x>-\dfrac{\pi}{2}$のときを考える.
このとき$0<-x<\dfrac{\pi}{2}$だから先の定理より
$$\cos(-x)< \dfrac{\sin(-x)}{-x}< 1$$
であるが, $\cos(-x)=\cos x$, $\sin(-x)=-\sin x$より,
$$\cos x< \dfrac{\sin x}{x}< 1$$
が得られる.
$\cos x<\dfrac{\sin x}{x}<1$が成り立つことが分かったが,
最左辺, 最右辺の$x\to 0$での極限は共に$1$なので,
挟み撃ちの原理より,
$$\lim_{x\to 0}\dfrac{\sin x}{x}=1$$
が成り立つ.
- $(\sin x)^\prime=\cos x$
- $(\cos x)^\prime=-\sin x$
別証明 $$\begin{align} &\big(\sin x\big)^\prime \underset{微分の定義}{=}\lim_{h\to 0}\dfrac{\sin(x+h)-\sin x}{h} \underset{加法定理}{=} \lim_{h\to 0}\dfrac{\sin x\cos h+\cos x\sin h-\sin x}{h}\\ =& -\sin x\lim_{h\to 0}\dfrac{1-\cos h}{h}+\cos x\lim_{h\to0}\dfrac{\sin h}{h} \underset{半角の公式}{=}-\sin x\cdot \lim_{h\to 0}\sin^2\left(\dfrac{h}{2}\right)+\cos x\cdot\lim_{ h\to 0}\dfrac{\sin h}{h}\\ =&-\sin x\cdot 0+\cos x\cdot 1 =\cos x \end{align}$$
別証明 加法定理から $$\cos x=\sin\left(\dfrac{\pi}{2}-x\right)\qquad \sin x=\cos\left(\dfrac{\pi}{2}-x\right)$$ が成り立つことが分かるから, $$\begin{align} &\big(\cos x\big)^\prime =\left(\sin\left(\dfrac{\pi}{2}-x\right)\right)^\prime \underset{合成の微分}{=}\cos\left(\dfrac{\pi}{2}-x\right)\cdot\left(\dfrac{\pi}{2}-x\right)^\prime\\ =&\cos\left(\dfrac{\pi}{2}-x\right)\cdot(-1) =-\sin x \end{align}$$ となる.
三角関数の変形公式を利用して, 2次関数$y=x^2$が焦点を持つこと, すなわち光(や音や熱など)が垂直に降りてくるとき, 反射した光が一点に集まることを示す.
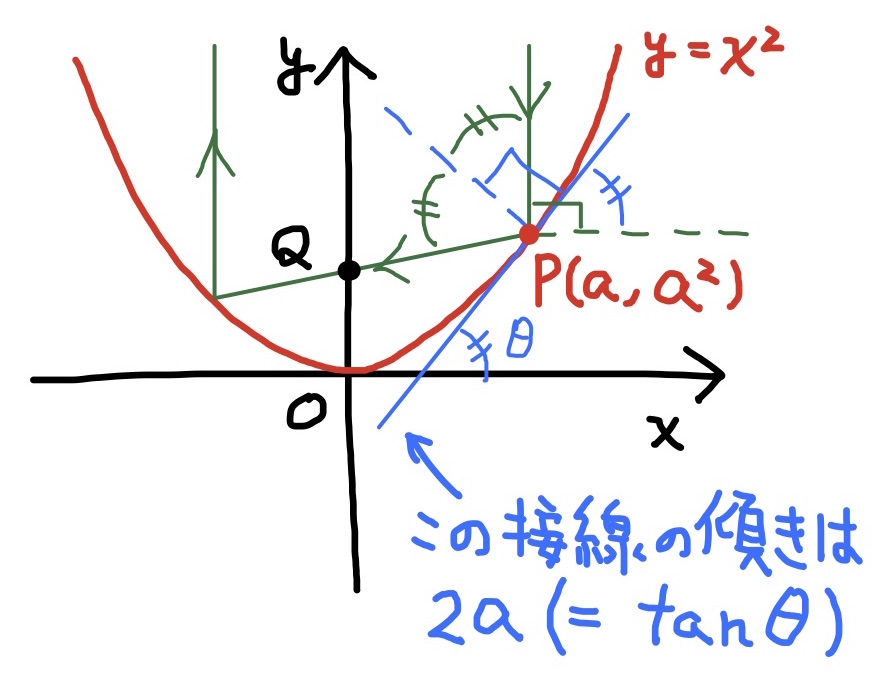
直線PQは点$P(a,a^2)$を通るから, $$y=t(x-a)+a^2\tag{1}$$ と表すことができる. ここで$t$は直線PQの傾きである. 傾き$t$を求めてみよう. 光が点$P$で反射するとき, 点$P$での2次関数の接線に対して入射角と反射角が等しくなるが, これらの角度は, ちょうど接線と水平線とのなす角$\theta$に等しいことが分かる. よって, 直線PQと水平線のなす角は $$2\theta-\dfrac{\pi}{2}$$ と表すことができる. この角度の正接は直線の傾き$t$であるから, $t=\tan\left(2\theta-\dfrac{\pi}{2}\right)$である. 接線の傾きは $$2a=\tan\theta\tag{2}$$ であることに注意して, 三角関数の色々な変形公式を使って計算すると $$\begin{align} t &=\tan\left(2\theta-\dfrac{\pi}{2}\right) =\dfrac{\sin\left(2\theta-\dfrac{\pi}{2}\right)}{\cos\left(2\theta-\dfrac{\pi}{2}\right)} \underset{加法定理}{=}\dfrac{\sin 2\theta\cos\dfrac{\pi}{2}-\cos 2\theta\sin\dfrac{\pi}{2}}{\cos 2\theta\cos\dfrac{\pi}{2}+\sin 2\theta\sin\dfrac{\pi}{2}}\\ =&-\dfrac{\cos 2\theta}{\sin 2\theta} \underset{倍角の公式}{=}-\dfrac{\cos^2 \theta-\sin^2\theta}{2\sin \theta\cos \theta} \underset{分母・分子を\cos^2\thetaで割る}{=}-\dfrac{1-\tan^2\theta}{2\tan\theta}\\ \underset{(2)より}{=}&-\dfrac{1-4a^2}{4a} =\dfrac{4a^2-1}{4a} \end{align}$$ となる. これを(1)に代入すれば, 直線PQの式は $$y=\dfrac{4a^2-1}{4a}(x-a)+a^2=\dfrac{4a^2-1}{4a}x+\dfrac{1}{4}$$ となることが分かる. よって, $y$切片は$\dfrac{1}{4}$であるから, 反射する点$P(a,a^2)$の位置に依存せず $$Q\left(0,\dfrac{1}{4}\right)$$ を通ることが分かる. この点Qが焦点である.
