日大工　総合教育　樋口幸治郎

工科系数学I及び演習(2017年度前期)

第7,8回　単調性と逆関数

Lorsque ces deux sciences se sont réunies,
elles se sont prêté des forces mutuelles,
et ont marché ensemble d'un pas rapide vers la perfection.
この二つの理論(代数と幾何)が手を取り合えば, 相補して完璧へと足を早めていく.

--- Leçons élémentaires sur les Mathématiques Joseph-Louis Lagrange
「数学初等講座」ジョゼフ=ルイ・ラグランジュ

前頁へ

次頁へ

単調性と逆関数

単調性と逆関数を学ぶ. (教科書p53-55)

• 単調性

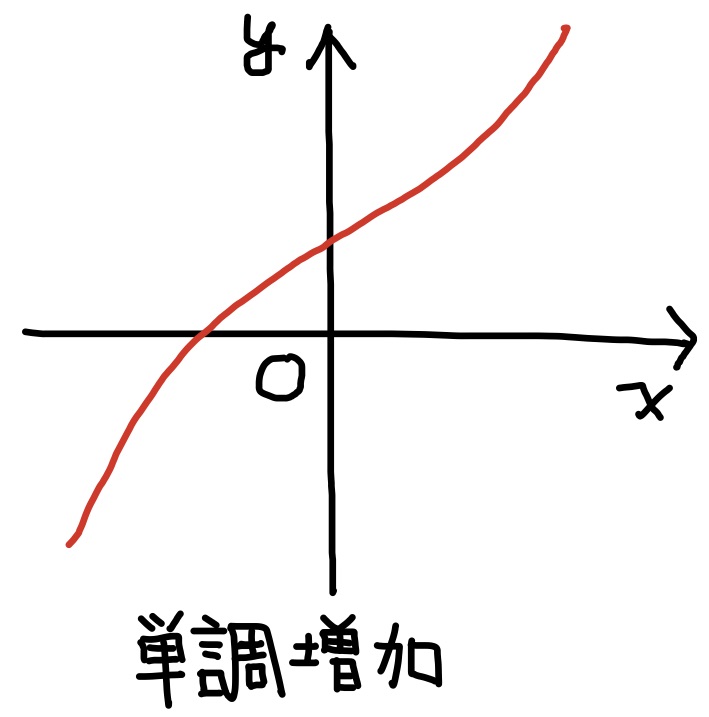
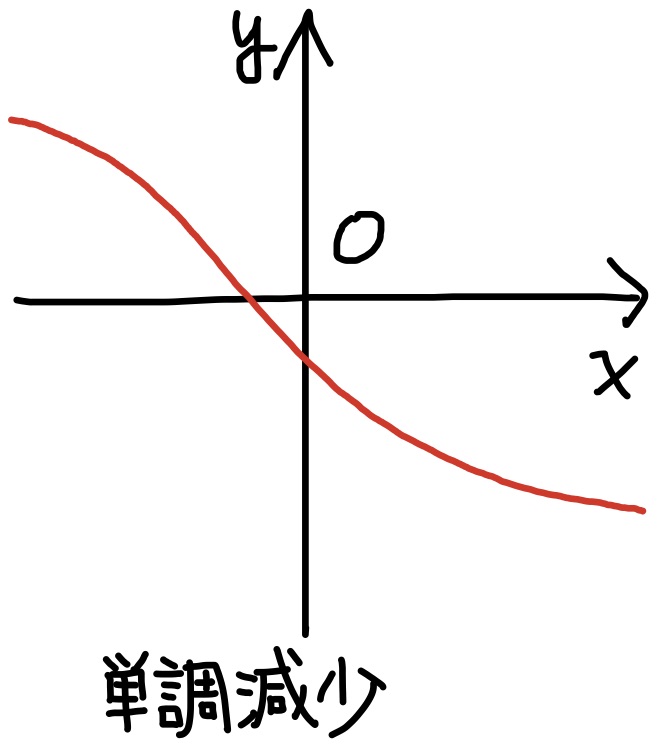
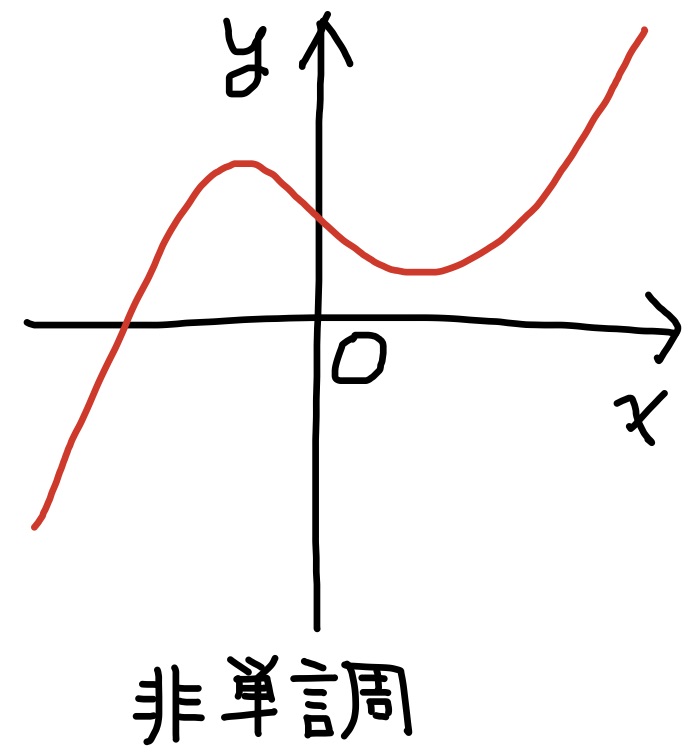
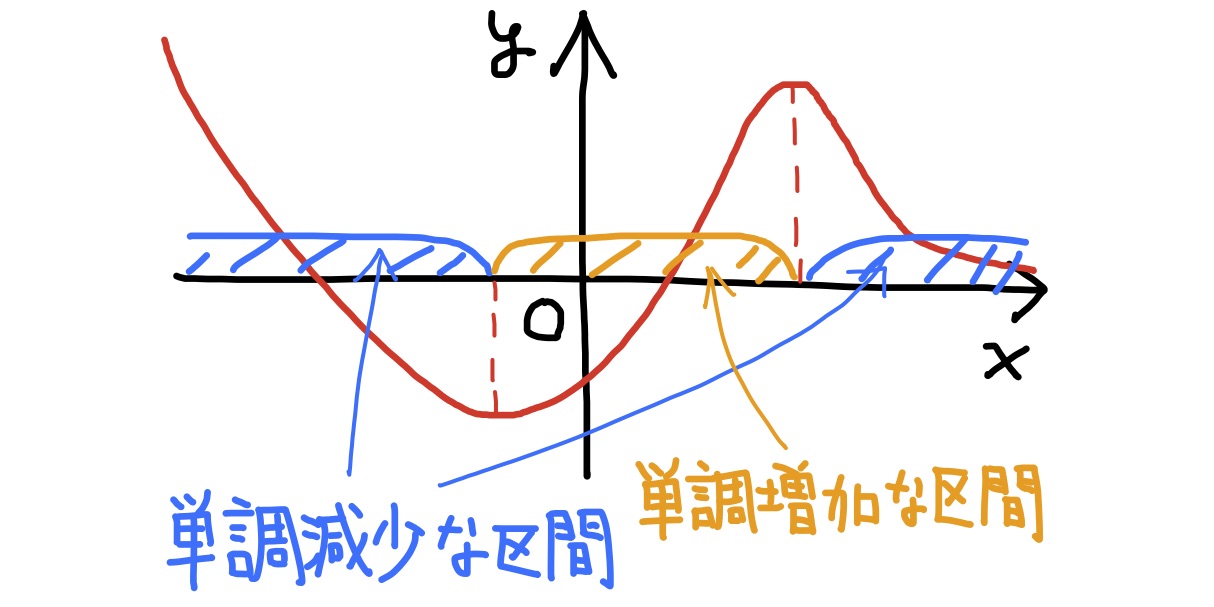
定義  関数$f(x)$について, $$x_1< x_2\quad\Longrightarrow\quad f(x_1)< f(x_2)$$ であるとき, 関数$f(x)$は単調増加であるという. また, $$x_1< x_2\quad\Longrightarrow\quad f(x_1)> f(x_2)$$ であれば, 単調減少という. 単調増加, 又は, 単調減少である関数を単調関数と言う. グラフについては, 単調増加関数は右上り, 単調減少関数は右下がりとなる.

関数をある区間に制限して単調性を論ずるときもよくある.

例  1. 関数$x, 3x, x^3, 2^x, \log_3 x$は全て単調増加関数
2. 関数$-x, -2x, -x^3, \left(\dfrac{1}{2}\right)^x, \log_{\dfrac{1}{3}} x$は全て単調減少関数
3. 関数$x^2$は区間$(-\infty,0]$で単調減少であり, 区間$[0,\infty)$で単調増加,
4. 関数$\sin x$は区間$\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$で単調増加. 関数$\cos x$は区間$\left[0,\pi\right]$で単調減少.


単調関数$y=f(x)$について, 値yに対してy=f(x)となるような実数xは(あれば)唯一つである. そこで以下のように関数$f(x)$の逆の対応(=逆関数)を考えることができる.

• 逆関数

定義  関数$y=f(x)$は, $$ 値yに対してy=f(x)となるような実数xは(あれば)唯一つ\tag{1} $$ であるとき, 関数$y=f(x)$での独立変数xと従属変数yの役割を入れ替えて, 独立変数$y$に対して$y=f(x)$を満たす従属変数$x$を対応させるような関数を考えることができる. これを関数$f(x)$の逆関数といい, $$x=f^{-1}(y)\quad または\quad f^{-1}(y)$$ で表す. 或いは, $x,y$を入れ替えて $$y=f^{-1}(x)\quad または\quad f^{-1}(x)$$ とも表す. またこのとき, $f(x)$は逆関数を持つという. 区間$I$上で(1)の条件が成り立つときには, $f(x)$は区間I上で逆関数を持つといい, その逆関数$f^{-1}(x)$を$f(x)$の区間I上の逆関数という.



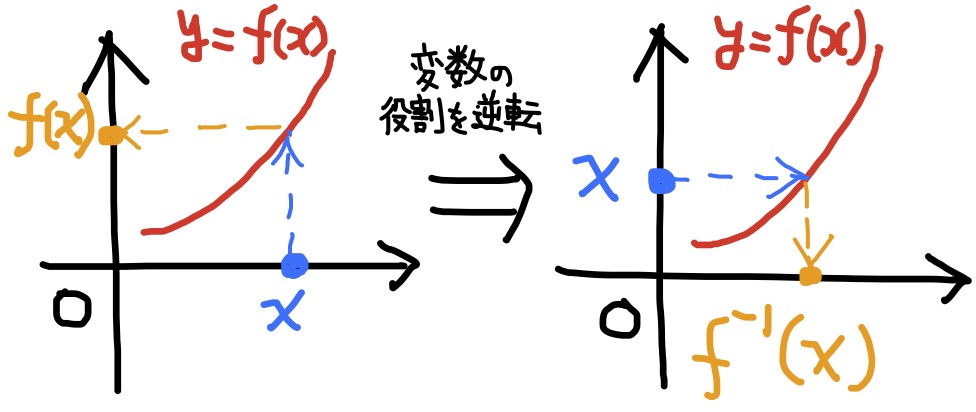
逆関数の定義から逆関数の値$f^{-1}(y)$は $$f^{-1}(y)=``f(x)=yとなるx"$$ という意味であり, 故に, $$y=f(x)\quad\iff\quad f^{-1}(y)=x\tag{2}$$ が成り立つ.

逆関数では$x$と$y$の役割が入れ替わるのだから, グラフにおいては$x$軸と$y$軸を入れ替えることに相当する. 従って, $y=f(x)$のグラフを直線$y=x$を軸に半回転させると$y=f^{-1}(x)$のグラフが得られる.



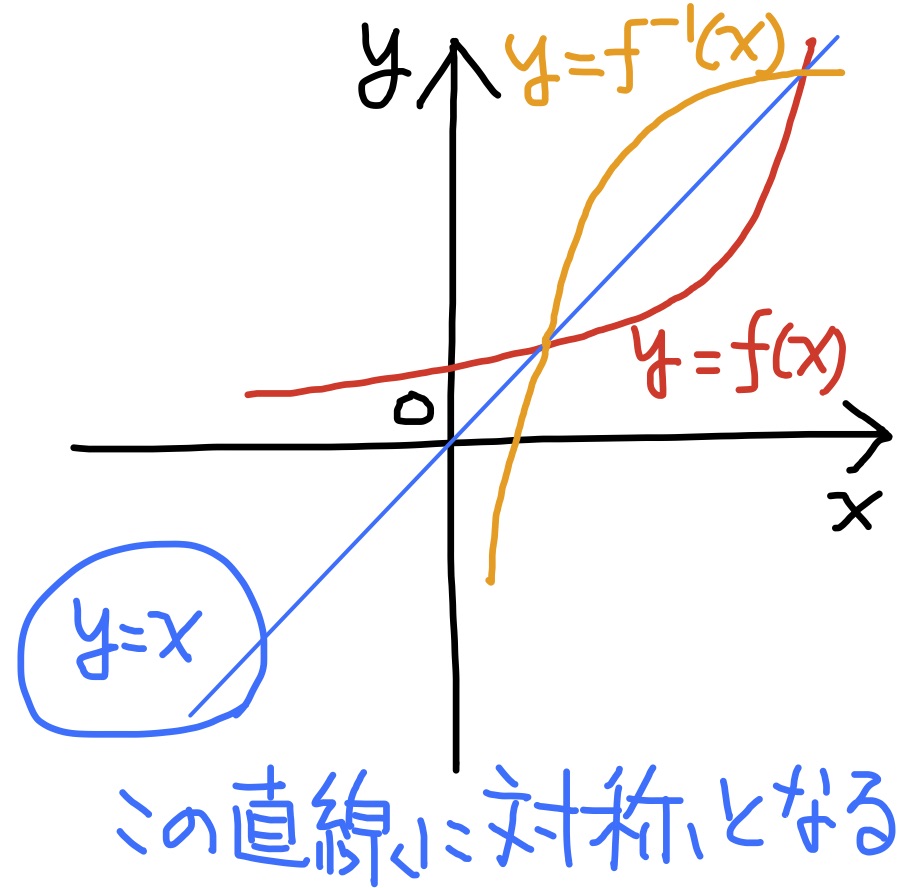
逆関数の逆はもとに戻る. つまり, $$(f^{-1})^{-1}(x)=f(x)$$ である. これはグラフでいうと, 直線$y=x$を軸に半回転を二回, つまり, 一回転することに相当するからである. 逆の逆が元通りなので, $$f(x)\quad \overset{逆}{\iff}\quad f^{-1}(x)$$ のようにある関数と逆関数の関係を書き表すこともある.

定理  逆関数を持つ関数$f(x)$について, $$f^{-1}(f(x))=x,\qquad f(f^{-1}(x))=x$$ が成り立つ.

証明  (2)より $$f^{-1}(f(x))=x\quad\iff\quad f(x)=f(x)$$ $$f(f^{-1}(x))=x\quad\iff\quad f^{-1}(x)=f^{-1}(x)$$ であるが, どちらも右辺は明らかに成り立つから, 左辺の等式も成り立つ.

例  $$足し算x+r\overset{逆}{\iff}引き算x-r\qquad 掛け算rx\overset{逆}{\iff}割り算\dfrac{x}{r}\qquad 自乗x^2\overset{逆}{\iff}平方根\pm\sqrt{x}$$ $$冪乗x^r\overset{逆}{\iff}冪乗根x^{\dfrac{1}{r}}\qquad 指数関数r^x\overset{逆}{\iff}対数関数\log_rx$$ $$三角関数\sin x,\cos x,\tan x\overset{逆}{\iff}逆三角関数\arcsin x,\arccos x,\arctan x$$ 因みに, より一般の関数(実数上の関数とは限らない対応関係)についても「逆」を考えることができ, 例えば, $$式の展開\overset{逆}{\iff}因数分解\qquad微分\overset{逆}{\iff}積分$$ である. 興味がある人は集合論や圏論を学ぶと良いだろう.

• 逆関数と連続性

定理  区間$I$上で定義された関数$f(x)$とその逆関数$f^{-1}(x)$について, $$f(x)は単調増加/単調減少\iff f^{-1}(x)は単調増加/単調減少$$ であり, また, $$f(x)は連続\iff f^{-1}(x)は連続$$ である.

証明  $f(x)$と$f^{-1}(x)$のグラフは直線$y=x$について対称であるから, $$グラフf(x)が右上がり/右下がり\iff グラフf^{-1}(x)が右上がり/右下がり$$ であり, $$グラフf(x)に飛びがない\iff グラフf^{-1}(x)に飛びがない$$ であるから, 定理が成り立つ.

• 逆関数と微分

定理  区間$I$上で微分可能な単調関数$f(x)$について, $f^\prime(f^{-1}(x))\ne 0$ならば, $f^{-1}(x)$も微分可能で, $$\Big(f^{-1}(x)\Big)^\prime =\left.\dfrac{1}{f^\prime(t)}\right|_{t=f^{-1}(x)} =\dfrac{1}{f^\prime(f^{-1}(x))}$$ が成り立つ.

証明  条件から$f^{-1}(x)$は連続であり, 関数$f(x)$と合成関数$f(f^{-1}(x))=x$は微分可能なので, 合成関数の微分定理から $$1=(x)^\prime=\Big(f(f^{-1}(x))\Big)^\prime=f^\prime(f^{-1}(x))(f^{-1}(x))^\prime$$ が成り立つ. 両辺を$f^\prime(f^{-1}(x))\ne 0$で割って, $$\Big(f^{-1}(x)\Big)^\prime=\dfrac{1}{f^\prime(f^{-1}(x))}$$ が得られる.

例  $(x^2)^\prime=2x$より$(\sqrt{x})^\prime=\left.\dfrac{1}{2t}\right|_{t=\sqrt{x}}=\dfrac{1}{2\sqrt{x}}$

微分についての補足

冪関数$x^q$についての微分公式と(教科書p7,p38,p41), 凸関数の微分可能性について学ぶ(教科書範囲外).

• 冪関数の微分

冪関数の微分公式$$(x^r)^\prime=rx^{r-1}\quad(rは有理数)\tag{1}$$ を段階的に証明する.

まず, $r$が自然数のとき等式(1)が成立する.

証明  等式$(x^n)^\prime=nx^{n-1}$を数学的帰納法で証明する. $(x^1)^\prime=(x)^\prime=1=1\cdot x^{1-1}$なので$n=1$のときは良い. $n=k$のときに等式の成立を仮定する(これを帰納法の仮定という)と $$(x^{k+1})^\prime=(x^kx)^\prime\underset{積の微分}{=}(x^k)^\prime x+x^k(x)^\prime \underset{帰納法の仮定}{=}kx^{k-1}x+x^k=kx^k+x^k=(k+1)x^k$$ となり, $n=k+1$のときも等式が成立する.

次に, $r$が整数のとき等式(1)が成立する.

証明  自然数のときは既に証明した. $r=0$のときは$$(x^0)^\prime=(1)^\prime=0=0x^{0-1}$$なので良い. $r$が負の整数$-n$のときは $$(x^r)^\prime=(x^{-n})^\prime =\left(\dfrac{1}{x^n}\right)^\prime \underset{逆数の微分}{=}-\dfrac{(x^n)^\prime}{(x^n)^2} =-\dfrac{nx^{n-1}}{x^{2n}} =-nx^{(n-1)-2n} =-nx^{-n-1} =rx^{r-1}$$ となるから, やはり等式(1)が成立する.

さらに, $r$が有理数のとき等式(1)が成立する.

証明  まず, $r=\dfrac{1}{n}$ ($n$は自然数)のときには, $$(x^r)^\prime =\left(x^{\dfrac{1}{n}}\right)^\prime =\left(\sqrt[n]{x}\right)^\prime \underset{逆関数の微分}{=}\left.\dfrac{1}{(t^n)^\prime}\right|_{t=\sqrt[n]{x}} =\left.\dfrac{1}{nt^{n-1}}\right|_{t=\sqrt[n]{x}} =\dfrac{1}{n(\sqrt[n]{x})^{n-1}} =\dfrac{1}{n}x^{\dfrac{1}{n}-1} =rx^{r-1} $$ となり等式(1)が成立する. この結果を使って, $r=\dfrac{k}{n}$ ($n$は自然数,$k$は整数)のときには, $$(x^r)^\prime =\left(x^{\dfrac{k}{n}}\right)^\prime =\left(\left(x^{k}\right)^{\dfrac{1}{n}}\right)^\prime \underset{合成関数の微分}{=}\left.(t^{\dfrac{1}{n}})^\prime\right|_{t=x^k}\cdot\left(x^k\right)^\prime =\dfrac{1}{n}(x^k)^{\dfrac{1}{n}-1}\cdot kx^{k-1} =\dfrac{k}{n}x^{\dfrac{k}{n}-1} =rx^{r-1} $$ となるから, やはり等式(1)が成立する.

• 凸性

定義  関数$y=f(x)$について, 任意の$a$について平均変化率 $$\dfrac{f(a+h)-f(a)}{h}$$ が$h$の関数として単調増加/単調減少であるとき, 関数$y=f(x)$は下に凸/上に凸であるという.



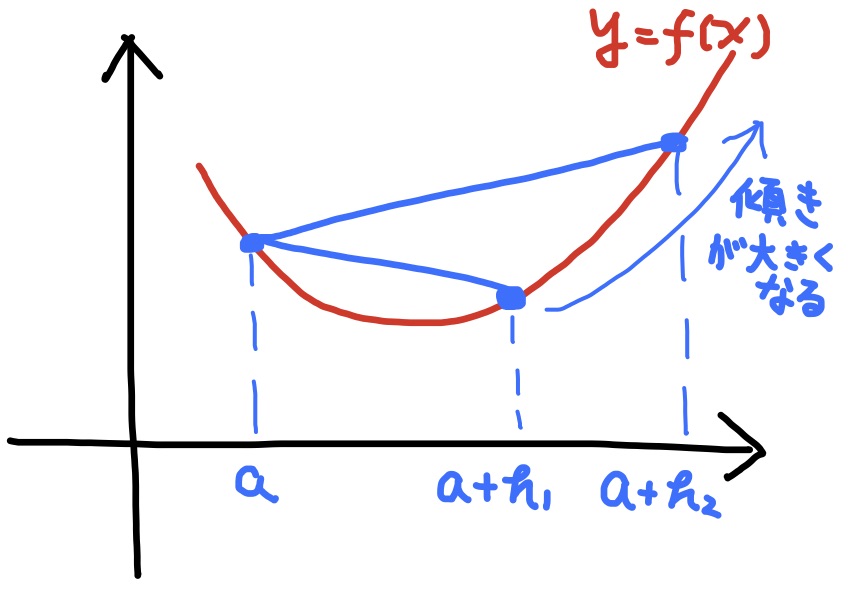
下に凸であることをグラフでいうと, 関数$y=f(x)$のグラフ上の任意の2点を結ぶ線分はグラフより上側にあることを意味する.

同様に, 上に凸であることをグラフでいうと, 関数$y=f(x)$のグラフ上の任意の2点を結ぶ線分はグラフより下側にあることを意味する.

• 凸性と微分

下に凸な関数$f(x)$の$x=a$での平均変化率$\dfrac{f(a+h)-f(a)}{h}$は$h$の関数として単調増加であるから, $h>0$のとき, $$\dfrac{f(a+(-h))-f(a)}{(-h)}<\dfrac{f(a+h)-f(a)}{h}$$ であり, $h\searrow 0$のとき, 左辺は単調に増加し, 右辺は単調に減少する. 従って, この両者の値が同じになっていくとき, つまり, $$\lim_{h\searrow 0}\dfrac{\left(\dfrac{f(a+h)-f(a)}{h}\right)}{\left(\dfrac{f(a+(-h))-f(a)}{(-h)}\right)}=1$$ のとき, 平均変化率は一定の値の収束する. つまり, $f(a)$は微分可能となる.

上記の議論は上に凸な関数についても同様である. 従って, 次が成り立つ.

定理  凸関数$y=f(x)$について, $x=a$について, $$\lim_{h\searrow 0}-\dfrac{f(a+h)-f(a)}{f(a-h)-f(a)}=1$$ が成り立てば, $f(x)$は$x=a$で微分可能である.

応用例 後に示すが, 指数関数$f(x)=2^x$は下に凸である. このことを仮定すると, 指数関数が微分可能であることが定理から示される. というのも $$\lim_{h\searrow 0}-\dfrac{f(x+h)-f(x)}{f(x-h)-f(x)} =\lim_{h\searrow 0}-\dfrac{2^{x+h}-2^x}{2^{x-h}-2^x} =\lim_{h\searrow 0}-\dfrac{2^{x+h}-2^x}{2^{x-h}-2^x}\cdot\dfrac{2^h}{2^h} =\lim_{h\searrow 0}-\dfrac{2^h(2^{x+h}-2^x)}{2^{x}-2^{x+h}} =\lim_{h\searrow 0}2^h =1$$ であるからである.

関数が凸であることを示すには, 次の定理が有用である.

定理  区間上で定義された連続関数$y=f(x)$について, 任意の$a,b$ ($a<b$)について $$f\left(\dfrac{a+b}{2}\right)<\dfrac{f(a)+f(b)}{2}$$ が成り立てば, 関数$y=f(x)$は下に凸である.

上記の不等式において「<」を「>」に置き換えた場合, 結論の「下に凸」は「上に凸」となる.

証明 下に凸であることはグラフ上の2点を結ぶどんな線分も必ずグラフより上側にあることを意味する. 従って, 任意の$u<w$について, 点$(u,f(u))$と点$(w,f(w))$を結ぶ線分を考えると, $u,w$の間の任意の数$v$について点$(v,f(v))$がその線分より下側にあることを示せば良い.
さて, 任意の$u<v<w$について, 次のように, 列$\{u_n\},\{w_n\}$を定義する: $$u_1=u,\qquad w_1=w,$$ $$u_2= \begin{cases} \dfrac{u_1+w_1}{2} & \dfrac{u_1+w_1}{2}\le vのとき\\ u_1 & \dfrac{u_1+w_1}{2}> vのとき \end{cases} \qquad w_2= \begin{cases} w_1 & \dfrac{u_1+w_1}{2}\le vのとき\\ \dfrac{u_1+w_1}{2} & \dfrac{u_1+w_1}{2}> vのとき \end{cases} $$ $$u_3= \begin{cases} \dfrac{u_2+w_2}{2} & \dfrac{u_2+w_2}{2}\le vのとき\\ u_2 & \dfrac{u_2+w_2}{2}> vのとき \end{cases} \qquad w_3= \begin{cases} w_2 & \dfrac{u_2+w_2}{2}\le vのとき\\ \dfrac{u_2+w_2}{2} & \dfrac{u_2+w_2}{2}> vのとき \end{cases} $$ 以下同様に$u_4,w_4,u_5,w_5,\cdots$を定義していく. 明らかに$u_n,w_n\to v$ ($n\to\infty$)である. 従って, 関数$y=f(x)$は連続だから, $$f(u_n),f(w_n)\to f(v) (n\to\infty)$$である.
さて, 定理の仮定 $$f\left(\dfrac{a+b}{2}\right)<\dfrac{f(a)+f(b)}{2}$$ から, グラフ上の点$\left(\dfrac{a+b}{2},f\left(\dfrac{a+b}{2}\right)\right)$は, 点$(a,f(a))$と点$(b,f(b))$を結ぶ線分の 中点$\left(\dfrac{a+b}{2},\dfrac{f(a)+f(b)}{2}\right)$より下側にあることがわかる. よって, 二点$(u_1,f(u_1)),(w_1,f(w_1))$を結ぶ線分より, 二点$(u_2,f(u_2)),(w_2,f(w_2))$を結ぶ線分は下側にあり, これよりも二点$(u_3,f(u_3)),(w_3,f(w_3))$を結ぶ線分は下側にあり, 以下同様, となる. したがって, その極限である点$(v,f(v))$は二点$(u,f(u)),(w,f(w))$より下側にある.

応用例 指数関数$f(x)=2^x$は下に凸であることを示そう. この関数は実数全体で定義されている連続な単調増加関数である. 定理から$a<b$について $$f\left(\dfrac{a+b}{2}\right)<\dfrac{f(a)+f(b)}{2}$$ を示せばよい. これは $$\dfrac{f(a)+f(b)}{2}-f\left(\dfrac{a+b}{2}\right)>0$$ と言い換えることができる. $$f(a)+f(b)-2f\left(\dfrac{a+b}{2}\right) =2^a+2^b-2\cdot 2^{\dfrac{a+b}{2}} =\left(2^{\dfrac{b}{2}}-2^{\dfrac{a}{2}}\right)^2 \underset{単調増加性}{>}0$$