平均値の定理を学び,
単調増加/減少な区間を調べる方法を学ぶ(教科書p85-86,p89-92).
- 平均値の定理
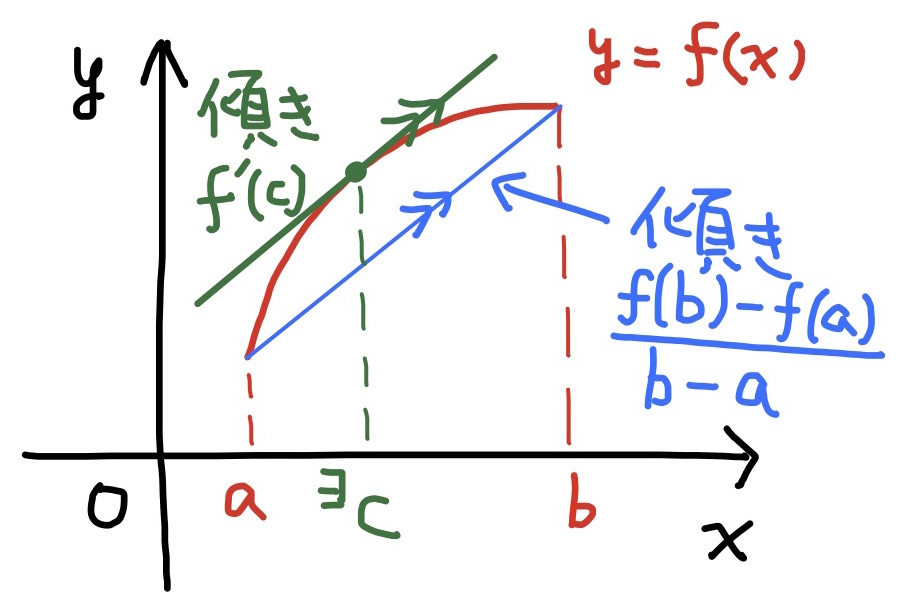
定理
$a<b$とする.
閉区間$[a,b]$で連続な関数$f(x)$が開区間$(a,b)$で微分可能とする.
このとき,
$$\dfrac{f(b)-f(a)}{b-a}=f^\prime(c)\qquad(a < {}^\exists c < b)$$
が成り立つ.
証明
関数$F(x)$を
$$F(x)=f(x)-\left(\dfrac{f(b)-f(a)}{b-a}(x-a)+f(a)\right)$$
と置く.
すると, $$F(a)=F(b)=0$$
が簡単な計算で確かめられる.
ロルの定理により
$$F^\prime(c)=f^\prime(c)-\dfrac{f(b)-f(a)}{b-a}=0\qquad(a<{}^\exists c<b)$$
が成り立つ.
式変形すれば
$$f^\prime(c)=\dfrac{f(b)-f(a)}{b-a}$$
である.
- コーシーの平均値の定理
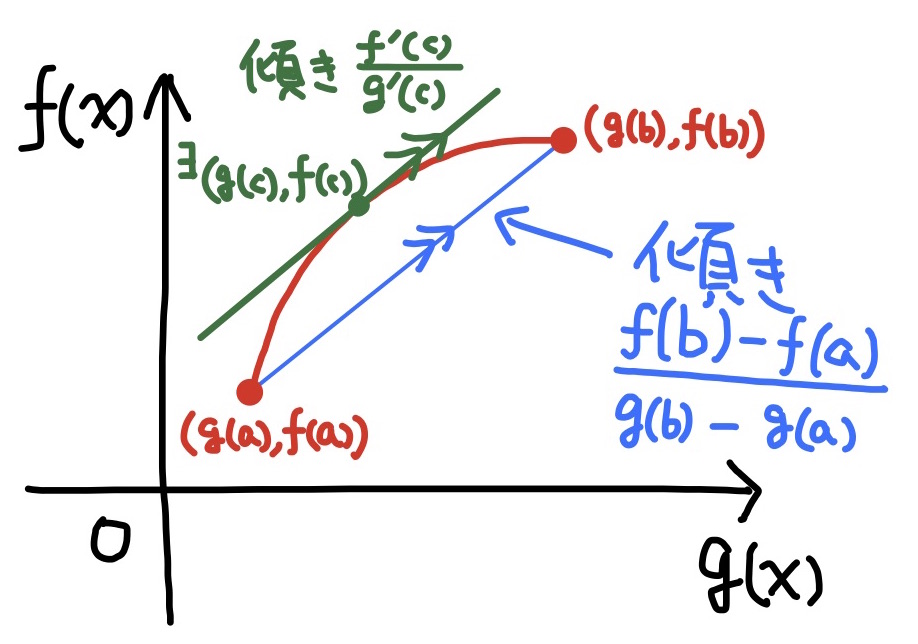
定理
関数$f(x),g(x)$と実数$a,b\quad$($a<b$)について
$$\dfrac{f(b)-f(a)}{g(b)-g(a)}=\dfrac{f^\prime(c)}{g^\prime(c)}\qquad(a<{}^\exists c<b)$$
が成り立つ.
但し$f(x),g(x)$は閉区間$[a,b]$で連続, 開区間$(a,b)$で微分可能であり, $g^\prime(x)\ne 0$ ($a<x<b$), $g(b)\ne g(a)$とする.
証明
関数$F(x)$を
$$F(x)=f(x)-\left(\dfrac{f(b)-f(a)}{g(b)-g(a)}(g(x)-g(a))+f(a)\right)$$
と置く.
すると, $$F(a)=F(b)=0$$
が簡単な計算で確かめられる.
ロルの定理により
$$F^\prime(c)=f^\prime(c)-\dfrac{f(b)-f(a)}{g(b)-g(a)}g^\prime(c)=0\qquad(a<{}^\exists c<b)$$
が成り立つ.
式変形すれば
$$\dfrac{f^\prime(c)}{g^\prime(c)}=\dfrac{f(b)-f(a)}{g(b)-g(a)}$$
である.
- 関数の増減
微分の値は接線の傾きであることを思えば,
微分が常に$+$なら単調増加, 常に$-$なら単調減少,
常に$0$, つまり接線はいつも水平線であれば定数,
となることは直感的に明らかであろう.
この事実は, 厳密には平均値の定理の帰結として導かれる.
定理
閉区間$[a,b]$で連続な$f(x)$は開区間$(a,b)$で微分可能であるとする. このとき,
$(a,b)$で常に
$f^\prime(x)
\left\{\begin{array}{c}
>\\
<\\
=
\end{array}\right\}
0
\qquad\Longrightarrow\qquad f(x)$は$[a,b]$で
$\begin{cases}
\mbox{単調増加}\\
\mbox{単調減少}\\
\mbox{定数}
\end{cases}$
証明
$a_1,b_1$を
$$a\le a_1<b_1\le b$$
となる任意の実数とする.
平均値の定理より,
$$f(b_1)-f(a_1)=(b_1-a_1)f^\prime(c)\qquad(a_1<{}^\exists c<b_1)\tag{1}$$
が成り立つ. 従って,
$$\begin{align}
&(a,b)で常に
f^\prime(x)
\begin{cases}
>0\\
<0\\
=0
\end{cases}
\qquad\Longrightarrow\qquad
(1)の右辺は
\begin{cases}
+\\
-\\
0
\end{cases}
\quad(a\le{}^\forall a_1<{}^\forall b_1\le b)
\\
& \qquad\Longrightarrow\qquad
\begin{cases}
f(a_1)<f(b_1)\\
f(a_1)>f(b_1)\\
f(a_1)=f(b_1)
\end{cases}
\quad(a\le{}^\forall a_1<{}^\forall b_1\le b)
\qquad\Longrightarrow\qquad
f(x)は(a,b)で
\begin{cases}
\mbox{単調増加}\\
\mbox{単調減少}\\
\mbox{定数}
\end{cases}
\end{align}$$
となる.
ここで, 記号「$\forall$」は「任意の」とか「全ての」を表す記号である.
例
1. 区間$(0,\pi)$で$\sin x<x$が成り立つことを示す.
$$f(x)=x-\sin x$$
とおけば,
$$f^\prime(x)=1-\cos x>0\qquad(0<{}^\forall x<\pi)$$
である.
よって, 関数$f(x)$は閉区間$[0,\pi]$で単調増加である.
$f(0)=0$であるから, 開区間$(0,\pi)$では
$$f(x)=x-\sin x>0$$
が成り立つ.
よって, 区間$(0,\pi)$で$\sin x<x$が成り立つ.
2. 区間$(0,\pi)$で$\cos x>1-\dfrac{1}{2}x^2$が成り立つことを示す.
$$g(x)=\cos x-\left(1-\dfrac{1}{2}x^2\right)=\cos x-1+\dfrac{1}{2}x^2$$
とおけば, 先ほどの結果から
$$g^\prime(x)=-\sin x+x=x-\sin x >0\qquad(0<{}^\forall x<\pi)$$
である.
よって, 関数$g(x)$は閉区間$[0,\pi]$で単調増加である.
$g(0)=0$であるから, 開区間$(0,\pi)$では
$$g(x)=\cos x-\left(1-\dfrac{1}{2}x^2\right)>0$$
が成り立つ.
よって, 区間$(0,\pi)$で$\cos x>1-\dfrac{1}{2}x^2$が成り立つ.
微分と単調性の関係を使って, 増減の表を書くことを学ぶ(教科書p89-97).
- 増減表
定義
関数$y=f(x)$について, その微分が$+$, $-$となる区間や微分が$0$になる位置,
及び, 微分の符号に応じて関数$y=f(x)$の増減をまとめた表を増減表という.
| $x$ |
$\cdots$ |
$a$ |
$\cdots$ |
$b$ |
$\cdots$ |
$c$ |
$\cdots$ |
| $f^\prime(x)$ |
$+$ |
$0$ |
$+$ |
$0$ |
$-$ |
$0$ |
$+$ |
| $f(x)$ |
$\nearrow$ |
$f(a)$ |
$\searrow$ |
$f(b)$ |
$\nearrow$ |
$f(c)$ |
$\nearrow$ |
上の表において, 矢印「$\nearrow$」と「$\searrow$」はそれぞれ単調増加, 単調減少であることを表す.
$x=a$での値$f(a)$は「$\nearrow$」と「 $\searrow$」との間(言わば山頂)にあるから極大値である.
$x=b$での値$f(b)$は「 $\searrow$」と「$\nearrow$」との間(言わば谷底)にあるから極小値である.
例
$y=x^3-4x^2-3x$の増減表を書く.
微分を求めると
$$y^\prime=3x^2-8x-3=(3x+1)(x-3)$$
であるから
$$y^\prime=0\iff x=3,-\dfrac{1}{3}$$
が分かる.
このとき関数の値は
$$y\big|_{x=3}=-18\qquad y\Big|_{x=-\dfrac{1}{3}}=\dfrac{14}{27}$$
である.
また, $x=3,-\dfrac{1}{3}$の前後での$y^\prime=(3x+1)(x-3)$の符号を求めると,
$x<-\dfrac{1}{3}$のとき$y^\prime$は$(-)\times(-)=(+)$であり,
$-\dfrac{1}{3} <x<3$のときは$y^\prime$は$(+)\times(-)=(-)$であり,
$x> 3$のときは$y^\prime$は$(+)\times(+)=(+)$である.
これらをまとめると, 増減表
| $x$ |
$\cdots$ |
$-\dfrac{1}{3}$ |
$\cdots$ |
$3$ |
$\cdots$ |
| $y^\prime$ |
$+$ |
$0$ |
$-$ |
$0$ |
$+$ |
| $y$ |
$\nearrow$ |
$\dfrac{14}{27}$ |
$\searrow$ |
$-18$ |
$\nearrow$ |
が得られる.
これから関数$y=x^3-4x^2-3x$は,
$x=-\dfrac{1}{3}$での値$\dfrac{14}{27}$は極大値であり,
$x=3$での値$-18$は極大値であることも分かる.
- 2回微分と極値
増減表において, 関数$y=f(x)$の微分$f^\prime(x)$の符号を直接求める代わりに,
2回微分を利用して間接的に求めることもできる.
定理
関数$y=f(x)$の2回微分$f^{\prime\prime}(x)$が存在して連続であれば,
$$f^\prime(a)=0かつf^{\prime\prime}(a)<0\quad\Longrightarrow\quad f(a)は極大$$
$$f^\prime(a)=0かつf^{\prime\prime}(a)>0\quad\Longrightarrow\quad f(a)は極小$$
が成り立つ.
証明
$$\begin{align}
&f^\prime(a)=0かつf^{\prime\prime}(a)<0
\quad\Longrightarrow\quad
(aに十分近いxについて)
x<aでf^\prime(x)>0,
x>aでf^\prime(x)<0 \\
&\Longrightarrow\quad
(aに十分近いxについて)
x<aでf(x)は単調増加
x>aでf(x)は単調減少
\quad\Longrightarrow\quad
f(a)は極大
\end{align}$$
である.
同様に,
$$\begin{align}
&f^\prime(a)=0かつf^{\prime\prime}(a)>0
\quad\Longrightarrow\quad
(aに十分近いxについて)
x<aでf^\prime(x)<0,
x>aでf^\prime(x)>0 \\
&\Longrightarrow\quad
(aに十分近いxについて)
x<aでf(x)は単調減少
x>aでf(x)は単調増加
\quad\Longrightarrow\quad
f(a)は極小
\end{align}$$
となる.
例
$f(x)=x^3-6x^2+9x-3$の増減表を書く.
1,2回の微分を求めると
$$f^\prime(x)=3x^2-12x+9=3(x-1)(x-3)\qquad f^{\prime\prime}(x)=6x-12$$
である.
$f^\prime(x)=0$となる$x$の値を求めると
$$f^\prime(x)=0\iff x=1,3$$
である.
このとき$f(x),f^{\prime\prime}(x)$の値は
$$f(1)=1, f^{\prime\prime}(1)=-6\qquad f(3)=-3, f^{\prime\prime}(3)=6$$
であるから, $f(1)$は極大, $f(3)$は極小である.
これらをまとめると, 増減表
| $x$ |
$\cdots$ |
$1$ |
$\cdots$ |
$3$ |
$\cdots$ |
| $y^\prime$ |
$+$ |
$0$ |
$-$ |
$0$ |
$+$ |
| $y$ |
$\nearrow$ |
$1$ |
$\searrow$ |
$-3$ |
$\nearrow$ |
が得られる.


