日大工　総合教育　樋口幸治郎

工科系数学I及び演習(2017年度前期)

第3,4回　極限と連続性

Les hommes meurent, mais leurs travaux restent.
人は死ぬが為したことは残る.

--- Augustin Louis Cauchy
オーギュスタン=ルイ・コーシーの最後の言葉

前頁へ

次頁へ

極限と連続性

極限と連続性の意味を学ぶ. また, 連続関数の重要な性質である中間値の定理を学ぶ. (教科書p1-3, p19-32)

• 収束

定義  値を変化させていく変数$x$が一定の値に近付くとき, $x$は収束するという. 近付く値を$a$とすれば, このとき, $$x\to a$$ と書き, $x$は$a$に収束するという. $x$が$a$より小さい/大きい値から近付く場合には「$x\nearrow a$」(又は「$x\to a-0$」)とか「$x\searrow a$」(又は「$x\to a+0$」)と書く.



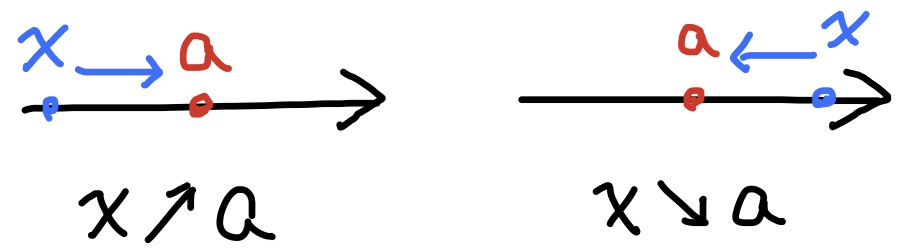
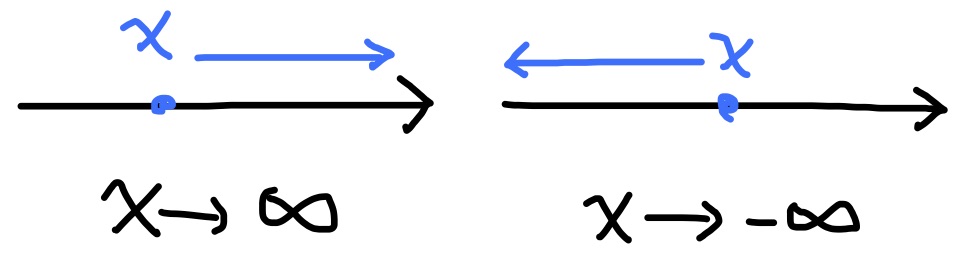
収束の対義語として発散という言葉を用いる. すなわち, 値を変化させていく変数$x$がどんな値にも近付いていかないとき, $x$は発散するという. 特別な場合として, $x$が限りなく大きく/小さくなっていくような発散は, $$x\to \infty\quad または\quad x\to -\infty$$ と書き, $x$は正/負の無限大に発散する, 或いは, $x$は正/負の無限大に近づくという.


• 極限と連続性

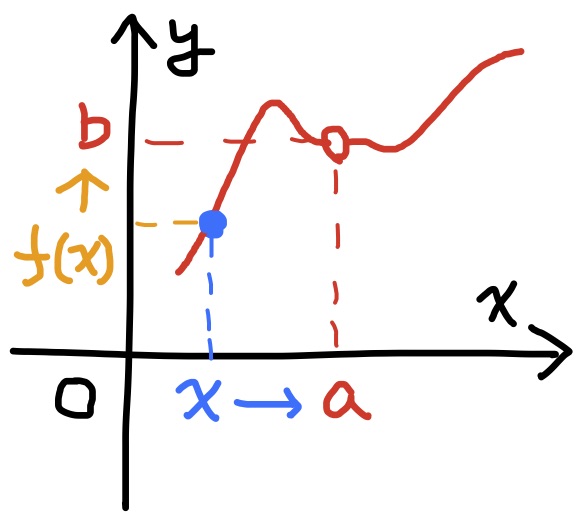
定義  定数$a,b$は実数, 又は, $\pm\infty$であるとする. 関数$f(x)$について, 変数$x$が$a$と異なる値を取りながら$a$に収束($a=\pm\infty$のときは発散)するとき, それに応じて関数$f(x)$の値が$b$に収束($b=\pm\infty$のときは発散)するとする, つまり, $$x\to a\quad (x\ne a)\quad\Longrightarrow\quad f(x)\to b$$ であるとする. これを単純に $$f(x)\to b\quad (x\to a)$$ と書き, また, $b$を$x\to a$のときの$f(x)$の極限とか極限値といい, $$b=\lim_{x\to a}f(x)$$ で書き表す.

$x\searrow a$や$x\nearrow a$と近付き方に制限を加えて, 右極限$\displaystyle\lim_{x\searrow a}f(x)$, 左極限$\displaystyle\lim_{x\nearrow a}f(x)$を考えることもある.

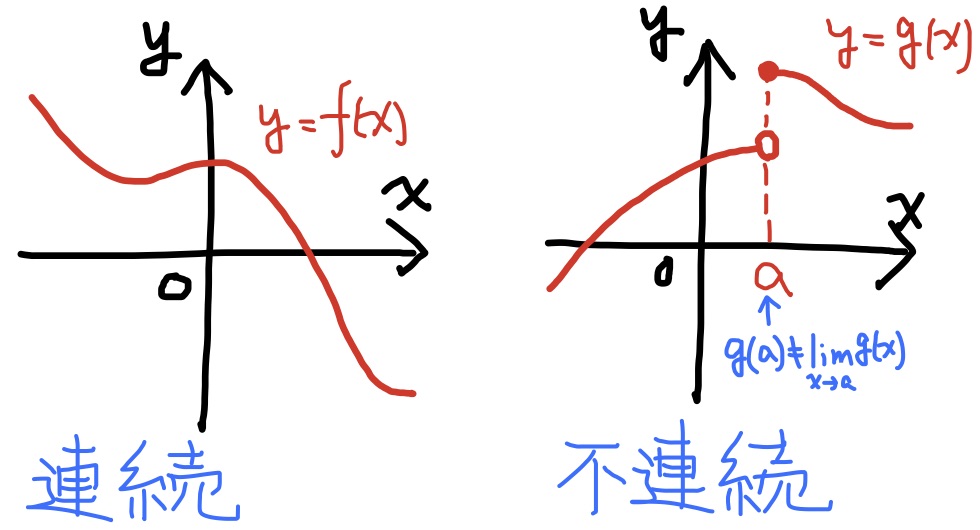
$f(x)\to f(a)$ ($x\to a$) であるとき, つまり, $$\displaystyle f(a)=\lim_{x\to a}f(x)$$であるとき, 関数$f(x)$はx=aで連続であるという. 定義域上のどの点aにおいても$f(x)$が$x=a$で連続であるとき, 関数$f(x)$を連続関数と呼ぶ.

連続関数のグラフには飛びがなく, 逆に不連続関数のグラフには飛びがある.



例  1. よく出てくる関数は大体連続関数である. 例えば $$冪関数x^r,\quad 指数関数r^x,\quad 対数関数\log_rx,\quad 三角関数\sin x, \cos x, \tan x$$ は連続関数である. これはグラフに飛びがないことから分かる. 従って, $$\lim_{x\to -1}x^4=(-1)^4=1,\quad \lim_{x\to 9}\log_3x=\log_3 9=2,\quad \lim_{x\to a}\sin x=\sin a$$ などのように, 極限の計算は単に変数xの近付く値を関数に代入するだけで良い. また, $$\lim_{x\to\infty}x=\infty,\quad \lim_{x\searrow \dfrac{\pi}{2}}\tan x=-\infty$$ であることがグラフから分かる.
2. 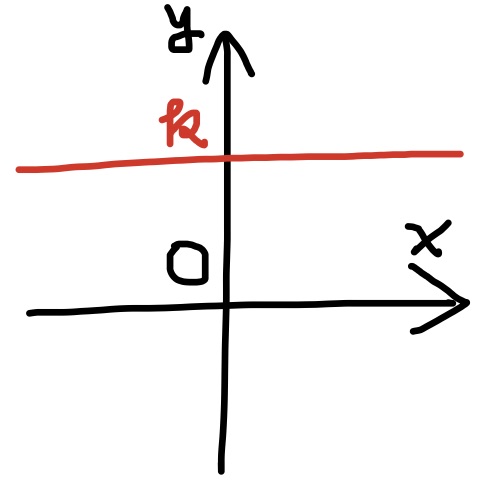定数関数は連続である. つまり, $k$を実数としたとき, どんな変数$x$の値に対しても関わらず$k$を関数の値とするような関数$y=k$は連続である. これもグラフを考えると容易に分かる. 従って, $$\lim_{x\to 2}5=5,\quad \lim_{x\to a}-1=-1,\quad \lim_{x\to b}k=k$$ のように極限を計算できる. また, $$\lim_{x\to\infty}k=k,\quad \lim_{x\to -\infty}k=k$$ である.
3. 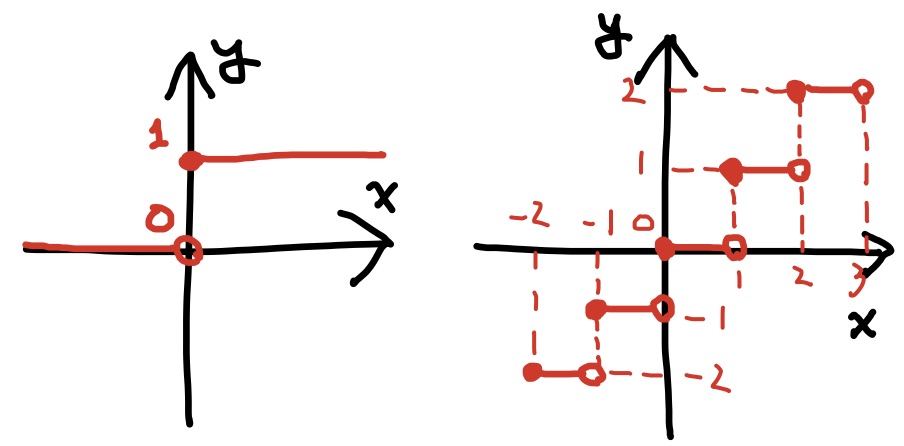(単位)ステップ関数$y=f(x)$とは, $$f(x)=\begin{cases} 1 & x\ge 0のとき \\ 0 & x< 0のとき \end{cases}$$ で定められる関数のことで, 不連続関数である($x=0$で不連続). $x=0$での左/右極限は, $$\lim_{x\nearrow 0}f(x)=0,\quad \lim_{x\searrow 0}f(x)=1$$ である. また, 床関数, 又は, ガウス関数$y=\lfloor x\rfloor$とは, $$\lfloor x\rfloor=``x以下の最大整数"$$ で定められる関数のことで, 不連続関数である(各整数の点で不連続). 関数$y=\lfloor x\rfloor$の整数$k$での左/右極限は, それぞれ, $k-1$と$k$である.
4. 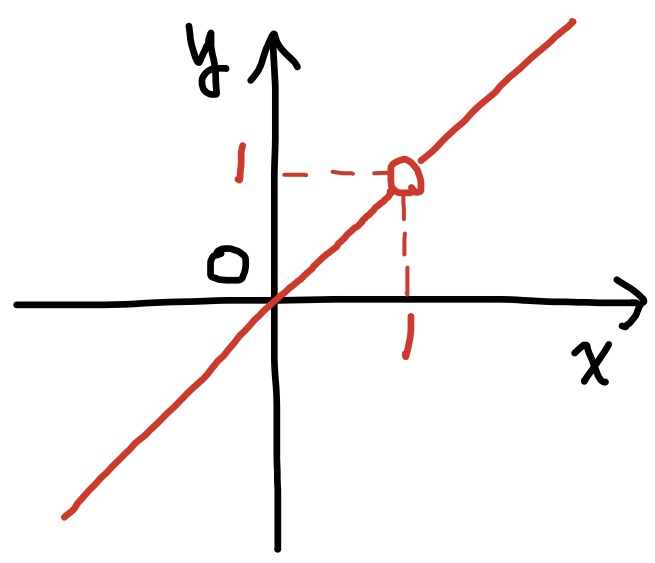関数$y=\dfrac{x(x-1)}{x-1}$は, $x=1$以外の実数を定義域とする関数である. ($x=1$を代入すると分母が$0$になり意味をなさない.) $x=1$では関数$y$は値を持たないが, $x\to 1$ ($x\ne 1$)のときの極限を考えることはできて, $$\lim_{x\to 1}\dfrac{x(x-1)}{x-1} \underset{約分して}{=}\lim_{x\to 1}x \underset{\because xの連続性}{=}1$$ である.


演習  1. 関数$y=|x|$のグラフを描き, この関数が連続か不連続か答えなさい.
2. 天井関数$y=\lceil x\rceil$は $$\lceil x\rceil=``x以上の最小整数"$$ で定められる関数のことである. このグラフを描き, この関数がどの点で不連続であるか答えなさい.


• イプシロン・デルタ論法

定数$a,b$は実数とすると, $f(x)\to b\ (x\to a)$であることは, $a$とは異なっていても$x$が$a$に十分近ければ$f(x)$が$b$に十分近いことを意味する. このことを近似的に等しいことを表す記号「$\fallingdotseq$」を用いて書けば, $$x\fallingdotseq a\ (x\ne a)\quad\Longrightarrow\quad f(x)\fallingdotseq b$$ と書ける. (ここで, $b=f(a)$とすれば$x=a$での連続性を表すことになる.)

この意味を厳密に述べるならば, 任意の正の実数$\varepsilon$に対して, 関数$f(x)$の値が$b$との誤差範囲を$\pm\varepsilon$とするには, 正の実数$\delta$を与えることができて, $a$と異なる$x$の$a$との誤差が$\pm\delta$であれば良い, という形で述べることができる. 「任意の」を表す記号「$\forall$」と「存在する」を表す記号「$\exists$」を用いて, 記号によって表すならば, $$(\forall\varepsilon>0)(\exists\delta>0)(\forall x\ne a)\Big[ |x-a|<\delta\quad\Longrightarrow\quad |f(x)-b|<\varepsilon\Big]$$ と書ける. (ここで, $b=f(a)$とすれば$x=a$での連続性を表すことになる.) この厳密な定義によって極限の性質を示していくことをイプシロン・デルタ論法という.

$a,b$の一方か両方が$\pm\infty$の場合も, 二つの正の実数$\varepsilon,\delta$を用いて同様の考え方で厳密に定義することができる. 例えば, $a$のみ$\infty$であれば, $$(\forall\varepsilon>0)(\exists\delta>0)(\forall x)\Big[ x>\delta\quad\Longrightarrow\quad |f(x)-b|<\varepsilon\Big]$$ と書ける.

• 区間

関数$f(x)$について, 独立変数$x$の動く範囲を区間に制限して考察することで, 関数$f(x)$の振る舞いが明確になることがある.

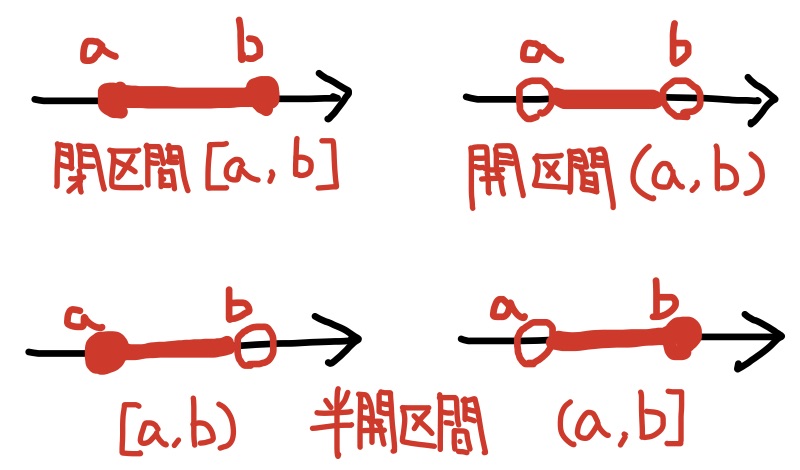
定義  二つの数$a,b$ ($\pm\infty$でもok)の間の範囲を区間という. 区間の範囲に端点を含めるときは鉤括弧「$[$」「$]$」を, 端点を含めないときは丸括弧「$($」「$)$」を用いて, 区間を $$[a,b],\quad (a,b),\quad [a,b),\quad (a,b]$$ のように表し, $[a,b]$を閉区間, $(a,b)$を開区間, $[a,b)$や$(a,b]$を半開区間という.



関数$f(x)$について, 区間Iのどの点$a$についても$f(x)$が連続であるとき, $f(x)$は区間$I$上で連続であるという.

例  1. 閉区間$[0,3]$は$0$以上$3$以下の範囲を表す区間である. 単位ステップ関数は$[0,3]$上で連続な関数である.
2. 半開区間$[5,6)$は$5$以上で$6$未満の範囲を表す区間である. 床関数$\lfloor x\rfloor$は$[5,6)$上で連続な関数である.
3. 開区間$(-\infty,0)$は$0$未満の数の範囲を表す区間である. 単位ステップ関数は$(-\infty,0)$上においても連続な関数である.
4. 開区間$(-\infty,\infty)$は全ての数を範囲とする区間である. 関数$x,x^2,2^x,\sin x$などは$(-\infty,\infty)$上で連続な関数である.


• 中間値の定理

定理   $f(x)$は閉区間$[a,b]$上連続で, $f(a)\ne f(b)$とする. このとき, $f(a)$と$f(b)$の間にある任意の数$r$に対して, $$f(c)=r,\qquad a<{}^\exists c<b$$ が成り立つ.



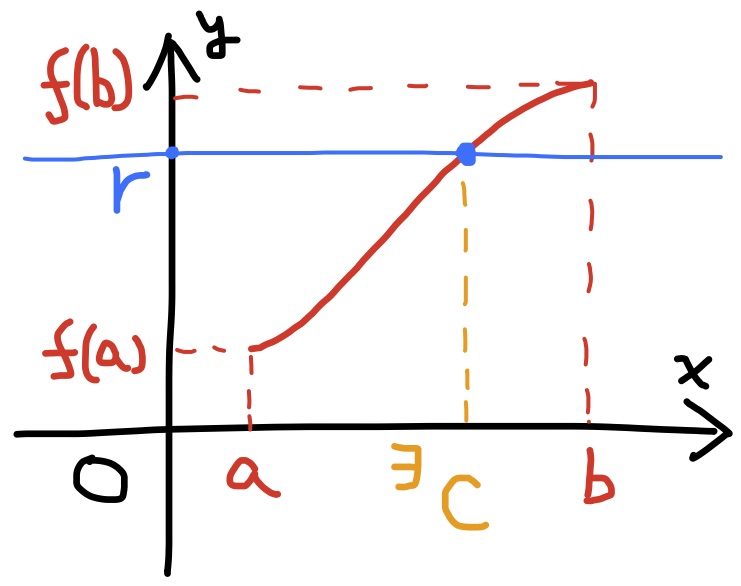
証明  $f(a)<f(b)$のときのみ示す. ($f(a)>f(b)$のときも同様に示せる.) $r$を$f(a),f(b)$の間の数なので, $f(a)< r< f(b)$である. $a,b$の間の数$c$で$f(c)=r$を満たすものを見つけることが目標である. (このとき, $a\le c\le b$であれば, $f(c)\ne f(a),f(b)$より必然的に $a<c<b$が成り立つことに注意しておこう. )
(i) $\ell_1=a, r_1=b$とおく. このとき, $f(\ell_1)\le r\le f(r_1)$である. (ii) $\ell_1$と$r_1$の中間の数$d$(つまり, $d=\dfrac{\ell_1+r_1}{2}$)において, $f(d)\le r$なら$\ell_2=d, r_2=r_1$と定め, そうでない(つまり, $f(d)>r$)ときは$r_2=d, \ell_2=\ell_1$と定める. 定め方から, $f(\ell_2)\le r\le f(r_2)$である. (iii) さらに$\ell_2$と$r_2$の中間の値$d$(つまり今度は, $d=\dfrac{\ell_2+r_2}{2}$)において, $f(d)\le r$なら$\ell_3=d, r_3=r_2$と定め, そうでない(つまり, $f(d)>r$)ときは$r_3=d, \ell_3=\ell_2$と定める. 定め方から, $f(\ell_3)\le r\le f(r_3)$である.
このように(ii)や(iii)のような作業を繰り返していけば, $$a=\ell_1\le \ell_2\le \ell_3\le......\le r_3\le r_2\le r_1=b$$ で, どの$\ell_n$,$r_n$についても $$f(\ell_n)\le r\le f(r_n)$$ であるような数列$\{\ell_n\},\{r_n\}$が得られる. 実数の完備性から $$a=\ell_1\le \ell_2\le \ell_3\le......\le c\le......\le r_3\le r_2\le r_1=b$$ であるような数$c$が存在する. この$c$が求める性質$f(c)=r$を持つことを示そう.
中間の値を選んで列$\{\ell_n\},\{r_n\}$を作っているのだから, $\ell_n$や$r_n$は$c$に近付いていく. しかも, $f(\ell_n)\le r\le f(r_n)$なので, 関数$f(x)$の連続性から$f(c)\le r\le f(c)$である. よって, $f(c)=r$が成り立つ.

中間値の定理の特別な場合として次の形の定理がよく使われる

定理   $f(x)$は区間$[a,b]$上で連続であり, f(a)とf(b)の符号が異なるとする. このとき, 方程式 $$f(x)=0$$ の実数解が$a$と$b$の間に(少なくとも一つ)存在する.



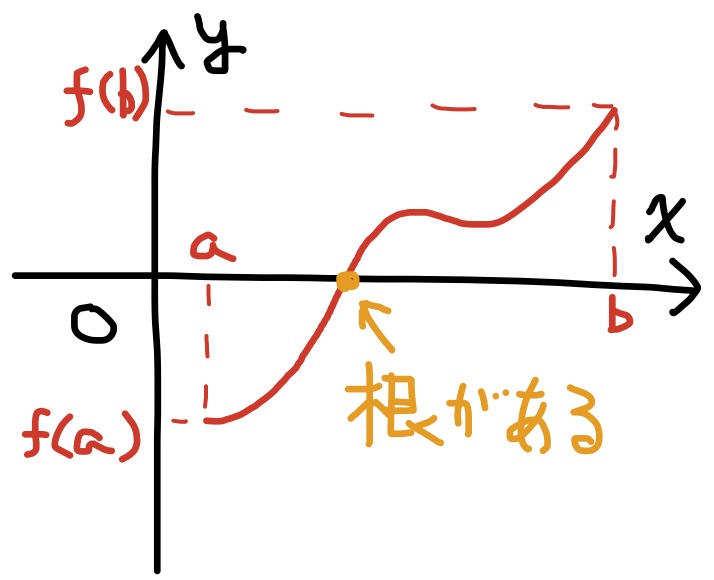
応用例. 方程式$x^4-6x^3+2=0$は $-1$と$1$の間に少なくとも一つの実数解を持つことを中間値の定理を用いて示す. $f(x)=x^4-6x^3+2$と置く. これは多項式だから区間$I=[-1,1]$でもちろん連続である. $f(-1)=(-1)^4-6(-1)^3+2=1+6+2=9$, $f(1)=1^4-6\cdot 1^3+2=1-6+2=-3$なので, 区間$I$の端点での値の符号は異なる. 従って与えられた方程式$f(x)=0$は$(-1,1)$の範囲で実数解を持つ.

極限の計算

極限の計算方法を学ぶ. (教科書p1-3, p19-32, p38-39)

• 極限と連続性の線形性

定理  関数の極限や連続性は線形性を持つ. つまり, $x\to a\ (x\ne a)$のとき$f(x),g(x)$は収束するものとし, $k$は定数とすれば, $$\displaystyle\lim_{x\to a}kf(x) =k\lim_{x\to a}f(x),\qquad \displaystyle\lim_{x\to a}\big(f(x)\pm g(x)\big) =\lim_{x\to a}f(x)\pm\lim_{x\to a}g(x)$$ が成り立ち, さらに, $f(x),g(x)$が$x=a$で連続であれば, 関数 $$kf(x),\qquad f(x)\pm g(x)$$ も連続である.

証明  $\displaystyle\lim_{x\to a}f(x)=b, \lim_{x\to a}g(x)=c$と置く. $x\to a$ ($x\ne a$)のとき, $f(x),g(x)$はそれぞれ$b,c$に近づくのだから, 定数倍$kf(x)$は$kb$に近づき, また, $f(x),g(x)$の和・差はそれぞれ$b+c,b-c$に近づく. $f(x),g(x)$が連続のときは$b=f(a)$, $c=f(a)$だから, これを代入すれば, $kf(x),f(x)\pm g(x)$の$x=a$での連続性が分かる.
(イプシロン・デルタ論法でより厳密に示すこともできる. ここでは, 極限に関する二つの等式をまとめたもの $$kf(x)+\ell g(x)\to kb+\ell c\ (x\to a)$$ をイプシロン・デルタ論法で示してみよう. 任意に正の実数$\varepsilon$を固定する. 示すべきは $$(\exists\delta>0)(\forall x\ne a)\Big[ |x-a|<\delta\quad\Longrightarrow\quad \left|\left(kf(x)+\ell g(x)\right)-\left(kb+\ell c\right)\right|<\varepsilon\Big]$$ である. $f(x)\to b$, $g(x)\to c$ ($x\to a$)だから, $|x-a|<\delta$のとき, $$|f(x)-b|<\dfrac{\varepsilon}{2|k|}\ (k\ne 0のとき),\qquad|g(x)-b|<\dfrac{\varepsilon}{2|\ell|}\ (\ell\ne 0のとき)$$ となるような正の実数$\delta$が存在する. 従って, $|x-a|<\delta$のとき $$\left|\Big(kf(x)+\ell g(x)\Big)-\Big(kb+\ell c\Big)\right|=\Big|k(f(x)-b)+\ell(g(x)-c)\Big|\le |k|\cdot|f(x)-b|+|\ell|\cdot|g(x)-c|<\dfrac{\varepsilon}{2}+\dfrac{\varepsilon}{2}=\varepsilon$$ となる. 以上で, $kf(x)+\ell g(x)\to kb+\ell c$ ($x\to a$)が示された. )

• 合成関数

定義  関数$y=f(g(x))$を$f(t)$と$g(x)$の合成関数という. (但し, $f(t),g(x)$は関数とする.)

例  1. 関数$(x^2+4)^5$は, 関数$t^5$に関数$x^2+4$を代入した合成関数である.
2. 関数$\dfrac{1}{x^3-1}$は, 関数$\dfrac{1}{t}$に関数$x^3-1$を代入した合成関数である.
3. 関数$\sqrt{x^2+x-5}$は, 関数$\sqrt{t}$に関数$x^2+x-5$を代入した合成関数である.
4. 関数$e^{3-2x}$は, 関数$e^t$に関数$3-2x$を代入した合成関数である.

合成関数の定義域については注意を要する. 例えば上の例2の合成関数$\dfrac{1}{x^3-1}$では, $x=1$のときは, $\dfrac{1}{1^3-1}=\dfrac{1}{0}$と分母が$0$になって意味をなさない. 合成関数$f(g(x))$の$x=a$での値$f(g(a))$が意味をなすのは, $$g(x)がx=aで値を持ち, f(t)がt=g(a)で値を持つ$$ ようなときである.

• 合成関数と極限

定理  関数$f(t),g(x)$について, $\displaystyle\lim_{x\to a}g(x)=b$かつ$f(t)$は$t=b$で連続ならば, $$\lim_{x\to a}f(g(x))=f(\lim_{x\to a}g(x))$$ が成り立つ. 特に, 二つの連続関数の合成は連続である.

証明  定理の等式を示すためには, $\displaystyle\lim_{x\to a}g(x)=b$だから, $x\to a$ ($x\ne a)$のとき$f(g(x))\to f(b)$であることを示せば良い. $t=g(x)$とおいて, $$x\to a\ (x\ne a) \underset{\because g(x)の収束性}{\Longrightarrow} t=g(x)\to b \underset{\because f(t)の連続性}{\Longrightarrow} f(g(x))=f(t)\to f(b) $$ であるから, 等式の成立が分かる. (ここで, $t=g(x)\to b$は$b$と異なる値を取りながら$b$に近付いていくとは限らない. これが$f(t)$が単に収束する以上に連続であることを仮定している理由である.) さらに$g(x)$が連続ならば $$\lim_{x\to a}f(g(x))=f(\lim_{x\to a}g(x))=f(g(a))$$ となるので, $f(g(x))$の連続性も分かる.

系  関数$f(x)$と自然数$n$について, $\lim_{x\to a}f(x)$が収束すれば, $$\lim_{x\to a}f(x)^n =\left(\lim_{x\to a}f(x)\right)^n,\quad \lim_{x\to a}\dfrac{1}{f(x)^n} =\dfrac{1}{\displaystyle\left(\lim_{x\to a}f(x)\right)^n} $$ が成り立つ, 但し後者については$\displaystyle\lim_{x\to a}f(x)\ne 0$かつ$f(x)\ne 0$ ($x$が$a$に十分近いとき)を仮定する. 従って, $f(x)$が$x=a$で連続ならば $$f(x)^n,\quad\dfrac{1}{f(x)^n}$$ も$x=a$で連続である.

証明  関数$t^n$や関数$\dfrac{1}{t^n}$が連続であるから, さきの定理から合成関数$f(x)^n,\dfrac{1}{f(x)^n}$についての極限の等式や連続性が導かれる.

• 極限/連続性と積・商

補題  $4f(x)g(x)=(f(x)+g(x))^2-(f(x)-g(x))^2$

定理  極限や連続性は積・商を保つ. つまり, $x\to a$ ($x\ne a$)のとき$f(x),g(x)$が収束するならば $$\displaystyle\lim_{x\to a}\big(f(x)g(x)\big) =\big(\lim_{x\to a}f(x)\big)\big(\lim_{x\to a}g(x)\big),\quad \displaystyle\lim_{x\to a}\left(\dfrac{f(x)}{g(x)}\right) =\dfrac{\displaystyle\lim_{x\to a}f(x)}{\displaystyle\lim_{x\to a}g(x)}$$ が成り立つ, 但し, 後者については$\displaystyle\lim_{x\to a}g(x)\ne 0$, $g(x)\ne 0$ ($x$が$a$に十分近いとき)と仮定する. 従って, 関数$f(x),g(x)$が$x=a$で連続ならば, $$f(x)g(x),\quad\dfrac{f(x)}{g(x)}$$も$x=a$で連続である.

証明  連続性についての主張は, 極限についての等式から直ちに得られるので, 極限についての等式のみ示せば良い. 議論の見やすさのために関数$f(x),g(x)$を単に$f,g$で表すことにする. 関数の積については, 補題や極限の線形性や先の系より $$4\lim_{x\to a}fg =\lim_{x\to a}(f+g)^2+\lim_{x\to a}(f-g)^2 =\left(\lim_{x\to a}(f+g)\right)^2+\left(\lim_{x\to a}(f-g)\right)^2$$ $$=\left(\lim_{x\to a}f+\lim_{x\to a}g\right)^2+\left(\lim_{x\to a}f-\lim_{x\to a}g\right)^2 =4\lim_{x\to a}f\lim_{x\to a}g$$ が得られる. よって, 両辺を$4$で割れば第一の等式が得られる. 第二の等式は, 今示したことと先の系より $$\lim_{x\to a}\dfrac{f}{g} =\lim_{x\to a}f\cdot\dfrac{1}{g} =\lim_{x\to a}f\cdot\lim_{x\to a}\dfrac{1}{g} =\lim_{x\to a}f\cdot\dfrac{1}{\displaystyle\lim_{x\to a}g} =\dfrac{\displaystyle\lim_{x\to a}f}{\displaystyle\lim_{x\to a}g} $$ と得られる.

• 不定形

色々な計算に現れる関数は, $$定数関数k, 冪関数x^r, 指数関数a^x, 対数関数\log_ax, 三角関数\sin x,\cos x,\tan x$$ などの基本的な連続関数たちに対し, 定数倍,四則演算や合成を繰り返して得られる関数であり, それらはこれまで見てきたことから連続であることが分かる. だから, そのような関数$f(x)$についての極限の計算では, $$\lim_{x\to a}f(x)=f(a)$$ と単に$f(x)$の$x$に$a$を代入して計算すれば良い. 但し, これはaが関数f(x)の定義域に入っている場合の話である. そうでないとき殆どの場合, $$\dfrac{0}{0},\qquad \dfrac{\pm\infty}{\pm\infty},\qquad \pm\infty\cdot 0$$ といった不定形と呼ばれる形や, $$\dfrac{a}{\pm\infty},\qquad \dfrac{\pm\infty}{a}\ (但しaは実数),\qquad \pm\infty\cdot b\ (但しbは0以外の実数か\pm\infty)$$ という定形と呼ばれる形が計算で現れる. 定形の場合, 最初のものは$0$に収束し, 後の二つは発散する. 不定形の場合には工夫が必要となる.

• 極限の計算

極限$\displaystyle\lim_{x\to a}f(x)$の計算は, 以下の手順で行えば良い.

1. $x=a$を関数に代入した値$f(a)$を計算する.
2. $f(a)$の計算過程で不定形 $$\dfrac{0}{0},\qquad \dfrac{\pm\infty}{\pm\infty},\qquad \pm\infty\cdot 0$$ が現れなければ, $f(a)=\displaystyle\lim_{x\to a}f(x)$で計算終了.
3. 不定形が現れるなら, f(x)を変形する.
4. 変形後の$g(x)$について, $g(a)$の計算で不定形がなければ$g(a)=\displaystyle\lim_{x\to a}f(x)$で計算終了. そうでなければ3に戻りやり直し.

上記の3番目での変形では, $x\ne a$の仮定のもとで$f(x)=g(x)$となるような変形法や, 後に学ぶロピタルの定理を使う, 微分を用いた変形法がある.

例. 1. 単に代入して計算できる例: $$\lim_{x\to 3}x^2=9,\quad \lim_{x\to -1}(x^3+5)=4,\quad \lim_{x\to 0}\dfrac{x^2-4}{x+9}=-\dfrac{4}{9}$$
2. 因数分解で変形する例: $$\lim_{x\to 2}\dfrac{x^2-4}{x-2}=\lim_{x\to 2}\dfrac{(x+2)(x-2)}{x-2}=\lim_{x\to 2}x+2=4$$
3. 通分で変形する例: $$\lim_{x\to 0}\dfrac{1}{x}\left(\dfrac{1}{2}+\dfrac{1}{x-2}\right) =\lim_{x\to 0}\dfrac{1}{x}\cdot\dfrac{x-2+2}{2(x-2)} =\lim_{x\to 0}\dfrac{1}{x}\cdot\dfrac{x}{2(x-2)} =\lim_{x\to 0}\dfrac{1}{2(x-2)} =\dfrac{1}{2(0-2)} =-\dfrac{1}{4} $$
4. 有理化で計算する例: $$\lim_{x\to 0}\dfrac{x}{\sqrt{x+1}-1}=\lim_{x\to 0}\dfrac{x(\sqrt{x+1}+1)}{(\sqrt{x+1}-1)(\sqrt{x+1}+1)}=\lim_{x\to 0}\dfrac{x(\sqrt{x+1}+1)}{x}=\lim_{x\to 0}(\sqrt{x+1}+1)=2$$


$x\to\infty$のときの極限はグラフを描くと分かることが多い.

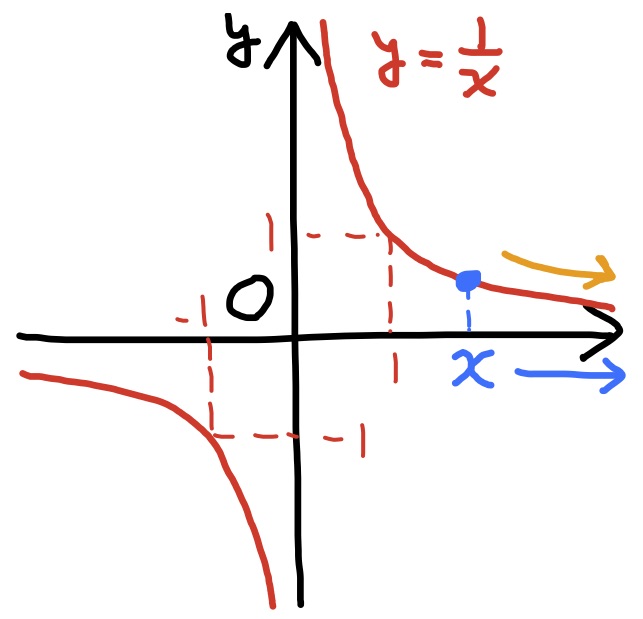
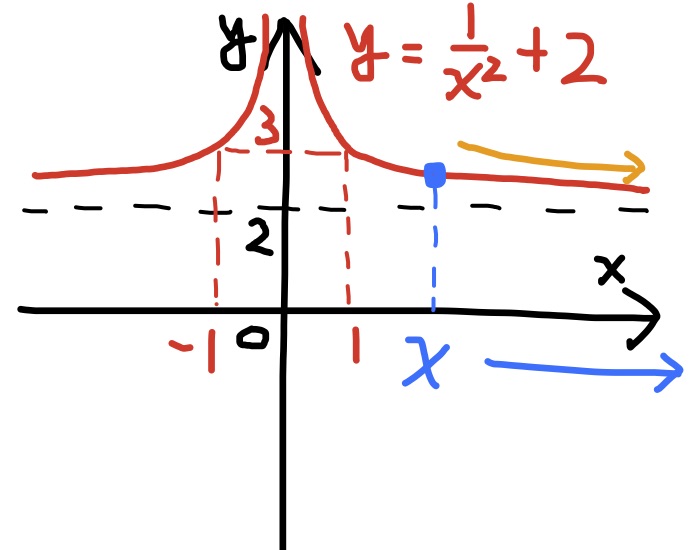
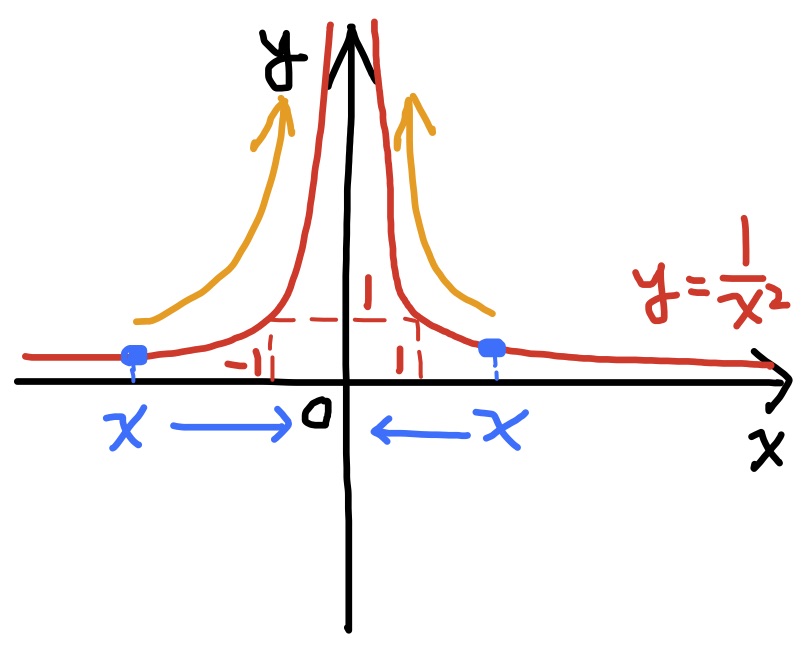
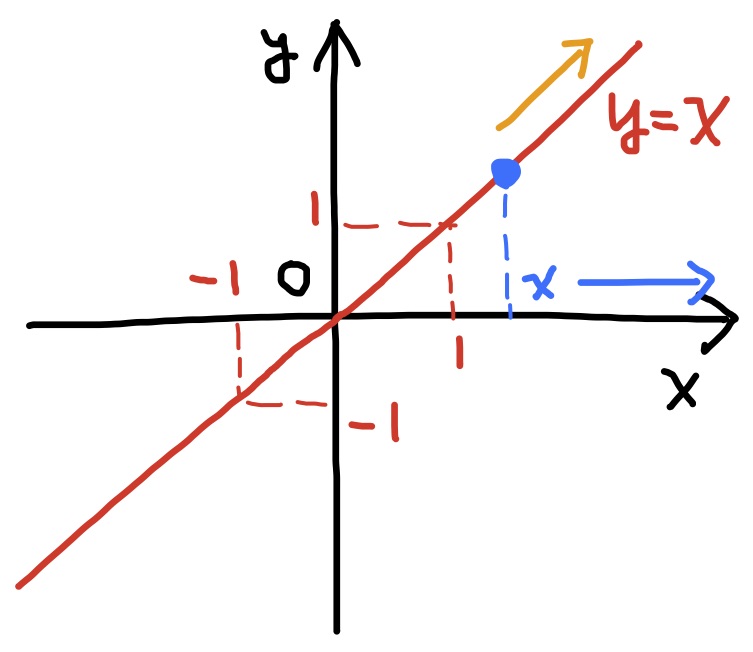
例. 1. $\displaystyle\lim_{x\to\infty}\dfrac{1}{x}=0$,$\qquad$ 2. $\displaystyle\lim_{x\to\infty}\left(\dfrac{1}{x^2}+2\right)=2$,$\qquad$ 3. $\displaystyle\lim_{x\to 0}\dfrac{1}{x^2}=\infty$,$\qquad$ 4. $\displaystyle\lim_{x\to\infty}x=\infty$.