逆三角関数の定義を学ぶ(教科書p56-60).
- 三角関数と単調性
三角関数$\sin x, \cos x, \tan x$は,
定義域全体では単調ではない.
しかし,
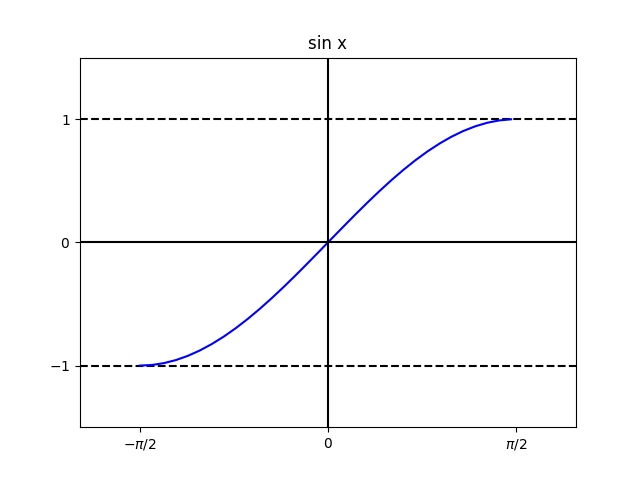
- $\sin x$は区間$\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$上で単調増加
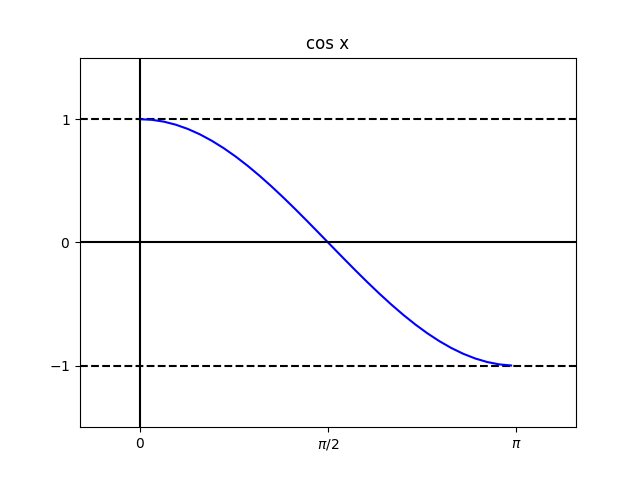
- $\cos x$は区間$[0,\pi]$上で単調減少
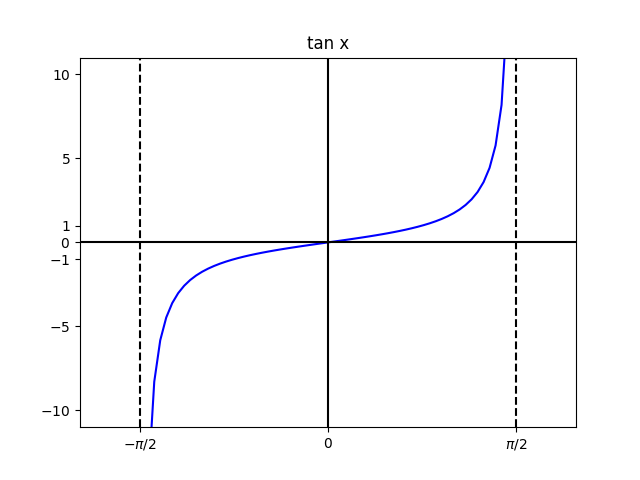
- $\tan x$は区間$\left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$上で単調増加
であるので,
それぞれの三角関数を上記の区間に制限すると逆関数を考えることができる.
- 逆三角関数
定義
三角関数$\sin x,\cos x,\tan x$をそれぞれ区間
$\left[-\dfrac{\pi}{2},\dfrac{\pi}{2}\right], [0,\pi], \left(-\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$に制限したときの逆関数を
$$\arcsin x,\qquad\arccos x,\qquad \arctan x$$
または
$$\sin^{-1} x,\qquad\cos^{-1} x,\qquad \tan^{-1} x$$
と書き,
それぞれ逆正弦関数, 逆余弦関数, 逆正接関数という.
(逆)三角関数の表記について,
$$\sin^{2}x=(\sin x)^2$$
である一方,
$$\sin^{-1}x\ne \dfrac{1}{\sin x}$$
である.
$\cos x$, $\tan x$についても同様で, 誤解しないように注意が必要である.
つまり$(\cdot)^2$は2乗を意味しているが$(\cdot)^{-1}$は逆関数(逆数ではない)を意味している.
定義から
$$\arcsin x=``\sin y=xかつ-\dfrac{\pi}{2}\le y\le \dfrac{\pi}{2}となる角度y"$$
$$\arccos x=``\cos y=xかつ0\le y\le \piとなる角度y"$$
$$\arctan x=``\tan y=xかつ-\dfrac{\pi}{2}< y< \dfrac{\pi}{2}となる角度y"$$
である.
また, 逆関数であることから,
$$\arcsin(\sin x)=x,\qquad \sin(\arcsin x)=x$$
$$\arccos(\cos x)=x,\qquad \cos(\arccos x)=x$$
$$\arctan(\tan x)=x,\qquad \tan(\arctan x)=x$$
である.
例
$\arcsin 1=\dfrac{\pi}{2},\quad\arcsin 0=0,\quad\arcsin \dfrac{\sqrt{3}}{2}=\dfrac{\pi}{3}$
$\arccos 1=0,\quad\arccos 0=\dfrac{\pi}{2},\quad\arccos \dfrac{\sqrt{3}}{2}=\dfrac{\pi}{6}$
$\arctan 1=\dfrac{\pi}{4},\quad\arctan 0=0,\quad\arctan \sqrt{3}=\dfrac{\pi}{3}$
- 逆三角関数のグラフ
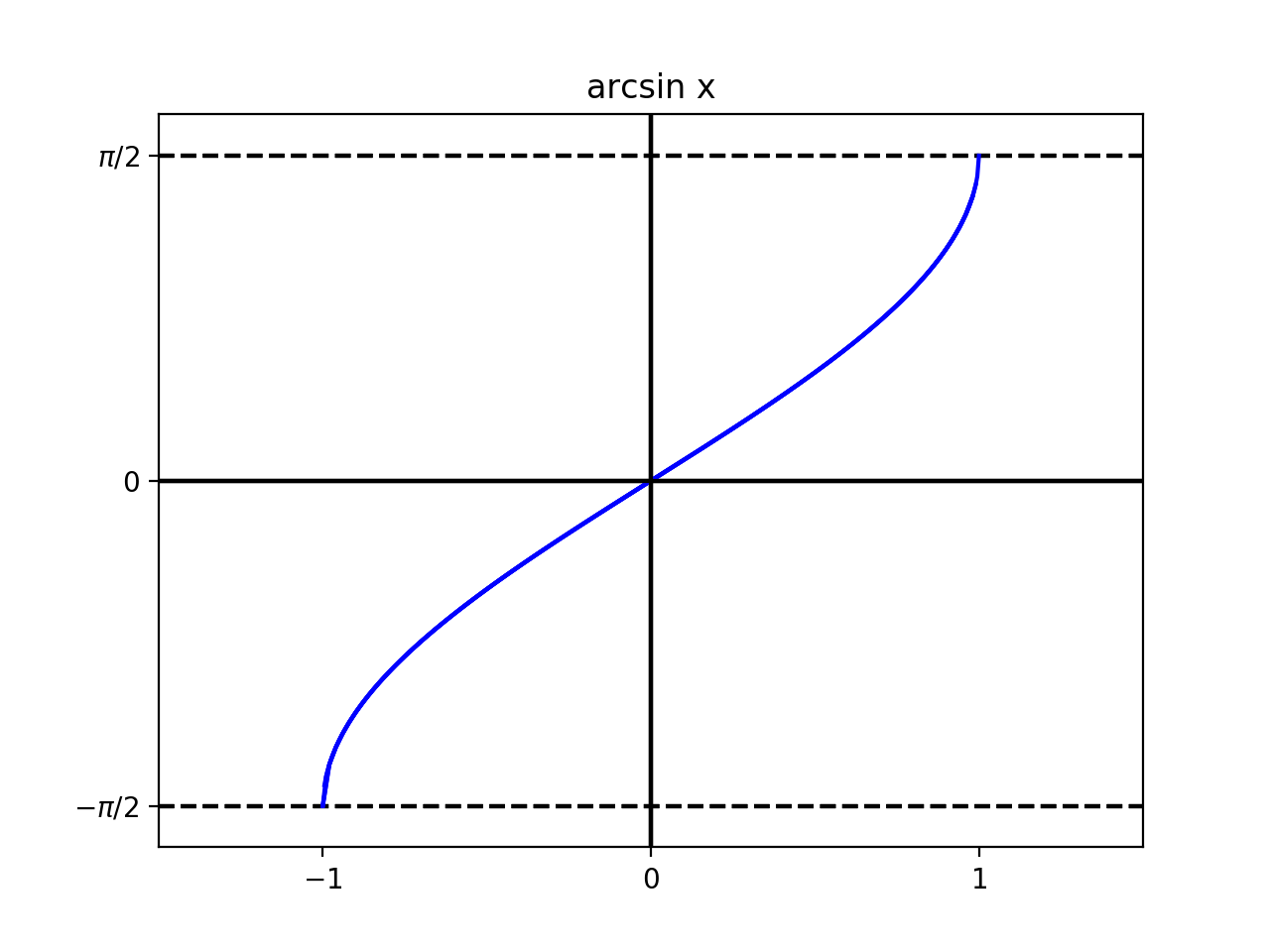
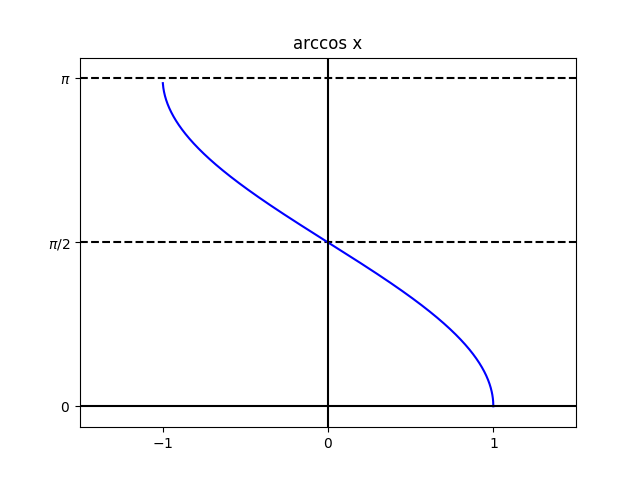
図からもわかるように, $\arcsin x$, $\arccos x$の定義域は$[-1,1]$であり,
$\arctan x$の定義域は実数全体$(-\infty,\infty)$である.
また, 逆三角関数は単調な連続関数である.
- 逆三角関数の公式
定理
$\arcsin x+\arccos x=\dfrac{\pi}{2}$
証明
$\arccos x=y$とおけば,
$$\arccos x=y
\underset{逆なので}{\iff} x=\cos y
\underset{\cos y=\sin(\dfrac{\pi}{2}-y)}{\iff} x=\sin(\dfrac{\pi}{2}-y)
\underset{逆なので}{\iff} \arcsin x=\dfrac{\pi}{2}-y$$
最後の式に$\arccos x=y$を代入して移行すれば,
$$\arcsin x+\arccos x=\dfrac{\pi}{2}$$
が得られる.
逆三角関数の微分を学ぶ(教科書p60-64).
- 逆三角関数の微分
定理
$\big(\arcsin x\big)^\prime=\dfrac{1}{\sqrt{1-x^2}}$
証明
$$\begin{align}
&\big(\arcsin x\big)^\prime
\underset{逆関数の微分}{=}\left.\dfrac{1}{(\sin t)^\prime}\right|_{t=\arcsin x}
\underset{正弦の微分}{=}\dfrac{1}{\cos(\arcsin x)}\\
\underset{\cos(\arcsin x)\ge 0}{=}&\dfrac{1}{\sqrt{\big(\cos(\arcsin x)\big)^2}}
\underset{\sin^2A+\cos^2A=1}{=}\dfrac{1}{\sqrt{1-\big(\sin(\arcsin x)\big)^2}}
\underset{\sin(\arcsin x)=x}{=}\dfrac{1}{\sqrt{1-x^2}}
\end{align}$$
定理
$\big(\arccos x\big)^\prime=-\dfrac{1}{\sqrt{1-x^2}}$
証明
$\arcsin x+\arccos x=\dfrac{\pi}{2}$であるから,
$$\big(\arccos x\big)^\prime
=\left(\dfrac{\pi}{2}-\arcsin x\right)^\prime
=-\dfrac{1}{\sqrt{1-x^2}}
$$
定理
$\big(\arctan x\big)^\prime=\dfrac{1}{1+x^2}$
証明
$$\big(\arctan x\big)^\prime
\underset{逆関数の微分}{=}\left.\dfrac{1}{\left(\tan t\right)^\prime}\right|_{t=\arctan x}
\underset{正接の微分}{=}\left.\dfrac{1}{\left(\dfrac{1}{\cos^2 t}\right)}\right|_{t=\arctan x}
\underset{1+\tan^2t=\dfrac{1}{\cos^2t}}{=}\dfrac{1}{1+\big(\tan(\arctan x)\big)^2}
=\dfrac{1}{1+x^2}
$$
を得る.
- 応用例
$(\arcsin 2x)^\prime=\dfrac{1}{\sqrt{1-(2x)^2}}\cdot(2x)^\prime=
\dfrac{2}{\sqrt{1-4x^2}}$
$(\arctan 3x)^\prime=\dfrac{1}{1+(3x)^2}\cdot(3x)^\prime=
\dfrac{3}{1+9x^2}$
$\left(\dfrac{1}{(\arcsin 3x)^2}\right)^\prime=
-\dfrac{\left((\arcsin 3x)^2\right)^\prime}{(\arcsin 3x)^4}=
-\dfrac{2(\arcsin 3x)\cdot(\arcsin 3x)^\prime}{(\arcsin 3x)^4}=
-\dfrac{2\cdot\left(\dfrac{1}{\sqrt{1-(3x)^2}}\right)\cdot(3x)^\prime}{(\arcsin 3x)^3}=
-\dfrac{6}{\sqrt{1-9x^2}(\arcsin 3x)^3}$
