日大工　総合教育　樋口幸治郎

工科系数学I及び演習(2017年度前期)

第1,2回　数と関数

Was beweisbar ist, soll in der Wissenschaft nicht ohne Beweis geglaubt werden.
科学において, 証明せらる事柄は証明なしに信ぜらるべからず.

--- Was sind und was sollen die Zahlen? Richart Dedekind
「数とは何かそして何であるべきか」リヒャルト・デデキント

前頁へ

次頁へ

数

自然数, 整数, 有理数, 実数, 複素数がどんなものであったか, ここで思い出すことにしよう. この講義の主役は実数である. しかし, 講義の後半に学ぶ三角関数について, それの色々な公式を覚え/思い出すとき, 複素数が役立つ. そこで, 講義では補助的に複素数の話も織り交ぜる. (教科書範囲外)

• 自然数(復習)

$$1,2,3,4,5,6,7,8,9,10,11,...$$ と個数を数えるときに現れる数を自然数という. 多くの本では$0$も自然数に含めるが, この講義では0は自然数に含めない.

• 整数(復習)

「2-5」や「7-15」のように自然数同士の引き算を行えるようにしようとすると $$-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10,11,...$$ という整数の概念が生まれる.

$0$より大きい数を正の数といい, $0$未満の数は負の数という. また, $0$以上/以下の数をそれぞれ非負/非正の数という.

• 有理数(復習)

「1$\div$3」や「-9$\div$13」のように0以外の整数同士の割り算を行えるようにしようとすると, $$\dfrac{1}{3}, -\dfrac{9}{13}, 0.5, -11, \dfrac{7}{5}, -5.86, 2.\dot{1}, ...$$ などのような有理数の概念が生まれる.

全ての有理数は, (i)整数同士の分数, つまり, $$\dfrac{m}{k}\quad (但し, m,kは整数, k\ne 0)$$ の形で書き表すことができ, また, 全ての有理数は(ii)循環小数で書き表すこともできる. (これらの表現は一意的ではない. 例えば$\dfrac{1}{2}=\dfrac{-3}{-6}$であり, また, $1.\dot{0}=0.\dot{9}$)

• 実数(復習)

$$3.14159265358979\cdots,\quad 1.41421356\cdots$$ などのように, 循環しない小数も数を表すようにしようとすると実数の概念が生まれる. 有理数でない実数は無理数と呼ばれる. 上記の円周率$\pi$や$\sqrt{2}$は無理数であることが証明できる.

全ての実数は, (i)小数展開, つまり, $$a.p_1p_2p_3p_4\cdots\quad (但し, aは整数, p_1,p_2,p_3,...は0以上から9以下の整数)$$ の形で書き表すことができる. 上記の$a$を整数部といい, $p_i$を小数第$i$位の値という. また, 実数は下図のように(ii)直線上の点で表すこともできる. このように実数を対応させた直線のことを実数直線, 又は, 数直線という.

実数の絶対値$|x|$は, 数直線において原点$0$と点$x$との間の長さを意味し, 二つの実数$x,y$の差の絶対値$|y-x|$は, 点$x$と点$y$の間の長さを意味する.
• 有理数の稠密性

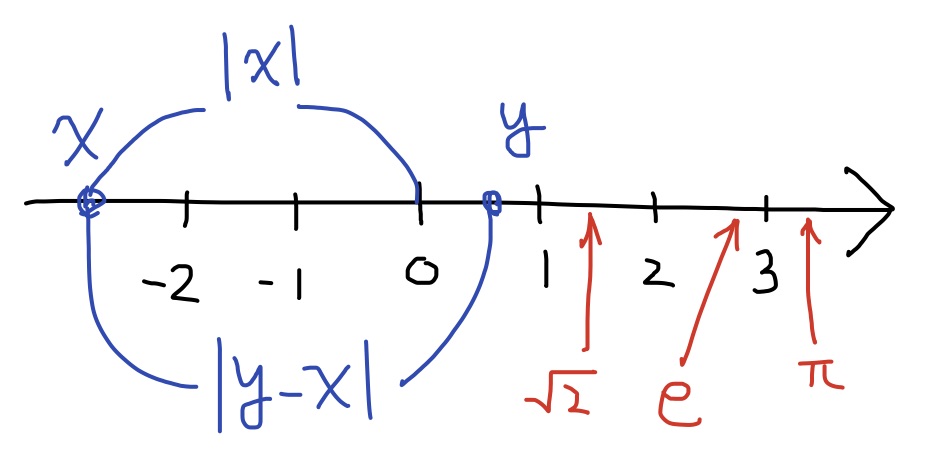
$$3,\ 3.1,\ 3.14,\ 3.141,\ 3.1415,\ 3.14159,...\tag{1}$$ は全て有理数であるが, その値はどんどん円周率に近づいていく. このように全ての実数は有理数で近似することができる. この事実を有理数の稠密性という.

• 有理数の非完備性

(1)は円周率を小さい値を取りながら近似しているが, $$4,\ 3.2,\ 3.15,\ 3.142,\ 3.1416,\ 3.14160,...\tag{2}$$ のように, 円周率よりも大きい値を取りながら近似していくこともできる. (1)に現れる全ての有理数以上の実数で, かつ, (2)に現れる全ての有理数以下の実数は, 円周率だけであり, これは無理数, つまり, 有理数ではない. この事実を有理数の非完備性という. これは言い換えると, $$\ell_1\le \ell_2\le \ell_3\le \ell_4\le ...... \le r_4\le r_3\le r_2\le r_1$$ を満たす有理数$\ell_1,\ell_2,\ell_3,\ell_4,...$と$r_1,r_2,r_3,r_4,...$に対し, $\ell_1,\ell_2,\ell_3,\ell_4..$以上で, $r_1,r_2,r_3,r_4...$以下である有理数は, 必ずしも存在しない, ということである.

• 実数の完備性

定理  実数は完備である. つまり, $$\ell_1\le \ell_2\le \ell_3\le \ell_4\le ...... \le r_4\le r_3\le r_2\le r_1\tag{3}$$ を満たす実数$\ell_1,\ell_2,\ell_3,\ell_4,...$と$r_1,r_2,r_3,r_4,...$に対し, $$\ell_1\le \ell_2\le \ell_3\le \ell_4\le ...\le{}^\exists u\le ... \le r_4\le r_3\le r_2\le r_1$$ である. (ここで, 記号「$\exists$」は(少なくとも一つ)存在することを表す.)



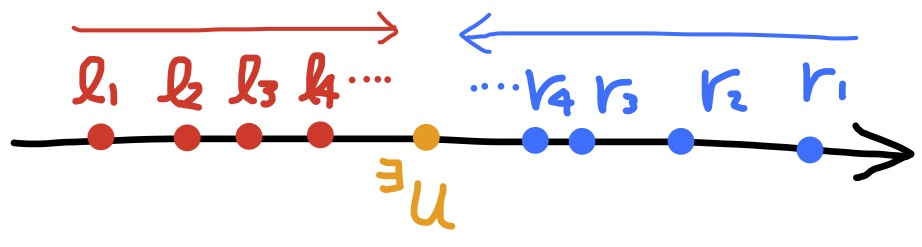
証明の概略  議論を簡単にするため(3)に現れる実数は全て正の実数と仮定する. (そうでない場合も以下と同じような考え方で証明できる.) $\ell_1,\ell_2,\ell_3,\ell_4..$たちの小数表現を用いて証明する. $$\ell_1,\ell_2,\ell_3,\ell_4..の整数部で最大の整数をa$$ とする. ($\ell_n\le r_1$よりそのような最大数が存在する.) 次に, $$\ell_1,\ell_2,\ell_3,\ell_4..のうち整数部がaである実数の小数第1位の最大数をp_1$$ とする. 次に, $$\ell_1,\ell_2,\ell_3,\ell_4..のうち小数第1位までがa.p_1である実数の小数第2位の最大数をp_2$$ とする. 次に, $$\ell_1,\ell_2,\ell_3,\ell_4..のうち小数第2位までがa.p_1p_2である実数の小数第3位の最大数をp_3$$ とする. 以下, 同様の議論により作られる小数表現 $$a.p_1p_2p_3p_4\cdots$$ が表す実数を$u$とすれば, $$\ell_1\le \ell_2\le \ell_3\le \ell_4\le ...\le u\le ... \le r_4\le r_3\le r_2\le r_1$$ が成り立つ.

• 複素数(復習)

$$x^2+1=0,\ x^2+2x+2=0$$ などのように, 全ての多項式が根を持つようにしようとすると複素数の概念が生まれる. $x^2+1=0$の解となる複素数の一つを $$i$$ と書き(本によっては「j」と書く), これを虚数単位という. $$i^2=-1$$ が成り立つので$i=\sqrt{-1}$とも書く.

全ての複素数は, (i)実部と虚部に分けた形, つまり, $$z=a+bi\quad (但し, a,bは実数)$$ の形で書き表すことができる. このとき, $${\rm Re}\ z=a,\quad {\rm Im}\ z=b$$ と書き, Re zを複素数zの実部, Im zをzの虚部という. 実数でない複素数は虚数と呼ばれ, そのうちでも, $$bi$$ と表される虚数は純虚数と呼ばれる. この表現における和・積は, $$(a+bi)+(c+di)=(a+c)+(b+d)i,\qquad (a+bi)(c+di)=(ac-bd)+(ad+bc)i$$ で与えられる. また, 複素数は下図のように(ii)平面上の点で表すこともできる. このように複素数を対応させた平面のことを複素平面, 又は, ガウス平面という.

複素数の絶対値$|z|=\sqrt{a^2+b^2}$は, 複素平面において原点$O$と点$z$との間の長さを意味し, 二つの複素数$z_1,z_2$の差の絶対値$|z_2-z_1|$は, 点$z_1$と点$z_2$の間の長さを意味する.

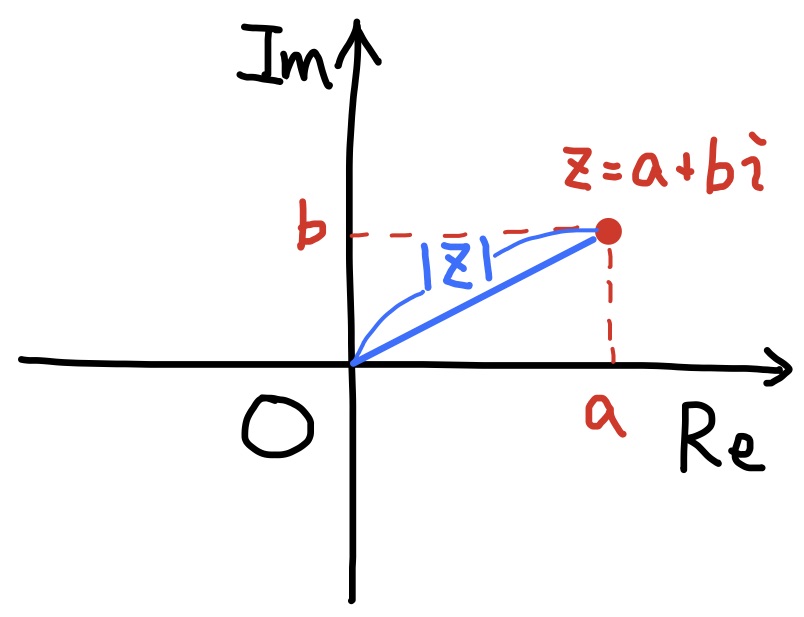
演習  $(5+3i)+(7-2i)=?$, $i-5i=?$, $(1-i)(3+2i)=?$, $2i\times (-3i)=?$, $|3+4i|=?$, $|-1+\sqrt{3}i|=?$

関数

関数やそのグラフ, また, 数列の意味を学ぶ. 多項式の特別な場合である1次関数や2次関数についての性質を復習する. (教科書範囲外)

• 関数,写像

定義  与えられた実数に対して, 唯一の実数を対応させる規則を実数上の関数とか, 実数上の写像という.

実数$x$に対して実数$y=f(x)$を対応させる関数は, $$ 関数y=f(x), 又は, 関数y, 又は, 関数f(x) $$ などと書き表す. (「$f(x)$」は, 値, 又は, 関数(=規則)を意味する場合があり, 多義語なので注意を要する.)

変数$x$を与えると$y=f(x)$の値が($x$に依存して)定まる, と考えているので, $x$を独立変数, $y$を従属変数という.

例  1. 関数$y=x^2$は, 実数$x$に対し実数$x^2$を対応させる実数上の関数である. これは多項式(=整式)が定める関数の例である.
2. 関数$x^3+4$は, 実数$x$に対し実数$x^3+4$を対応させる実数上の関数である. これも多項式(=整式)が定める関数の例である.
3. 三角関数の一つである正弦関数$v=\sin u$は, 実数$u$に対し実数$v=\sin u$を対応させる実数上の関数である. このように, 変数の文字は$x,y$でないこともある.
4. 実数$x$に対し実数$8$を対応させる規則は実数上の関数で, この定数関数は関数$y=8$とか, 関数$8$と書き表す.
5. 関数$y=\dfrac{1}{x}$は, 0でない実数$x$に対し実数$\dfrac{1}{x}$を対応させる実数上の関数である. このように, 一部の実数について対応のない関数もある.
6. 対数関数$y=\log_2 x$や関数$\dfrac{1}{\sqrt{x}}$は, 正の実数$x$に対し実数$\log_2 x$や$\dfrac{1}{\sqrt{x}}$を対応させる関数である.
7. 正の実数$x$に対し, 自乗が$x$になるような実数を対応させる規則は, 関数ではない. 何故なら, $x$に対応する実数は$\pm\sqrt{x}$で, 唯一ではないからである. このように複数の値が対応する規則はしばしば多値関数と呼ばれ, これも関数として扱う場合もあるが, この講義では多値関数は取り扱わない.

定義  関数$y=f(x)$によって対応付けられている実数の範囲を, 関数$y=f(x)$の定義域と呼ぶ.

例  関数$\dfrac{1}{x}$の定義域は0以外の実数, 関数$\log_2 x$や$\dfrac{1}{\sqrt{x}}$の定義域はどちらも正の実数である. また関数$y=x$の定義域は実数全体である.

与えられた複素数に対して, 唯一の複素数を対応させる規則は複素数上の関数とか, 複素数上の写像いう. また, もっと一般に, 与えられたモノに対して, 唯一のモノを対応させる規則は関数とか写像という. 例えば, 「微分」は実数上の関数に対して, 唯一の実数上の関数を対応させるような写像である. しかしながら, 講義に現れる関数は主に実数上の関数であるので, 簡便さのため, 特に断らない限り, $$「関数」とは「実数上の関数」$$ を表すことにする.

• 関数のグラフ・曲線

関数は, $y=f(x)$や$f(x)$のように(i)式で表すことができるが, 下図のように(ii)平面上のグラフ(=線)で表すこともできる.

図のような平面を(直交)座標平面, 又は, デカルト座標平面という.

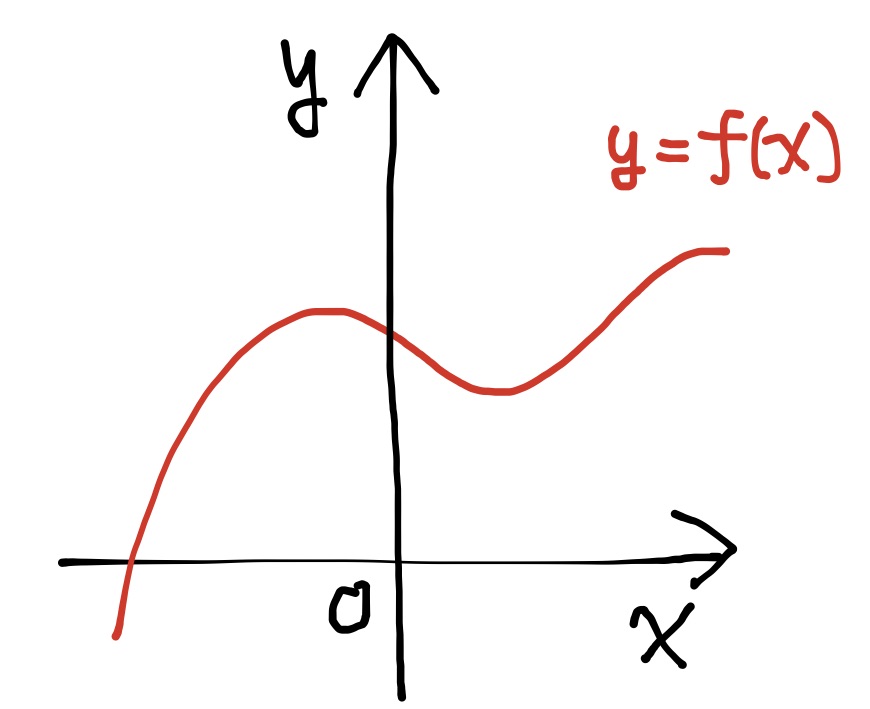
例  1. 関数$y=x+2$のグラフ


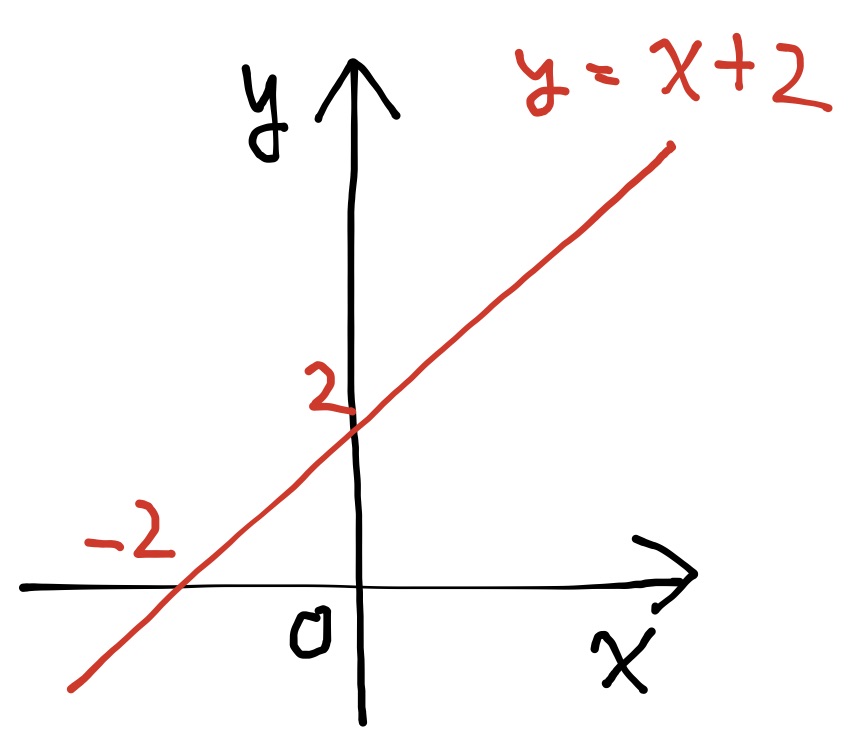
2. 関数$y=x^2$のグラフ



• 数列

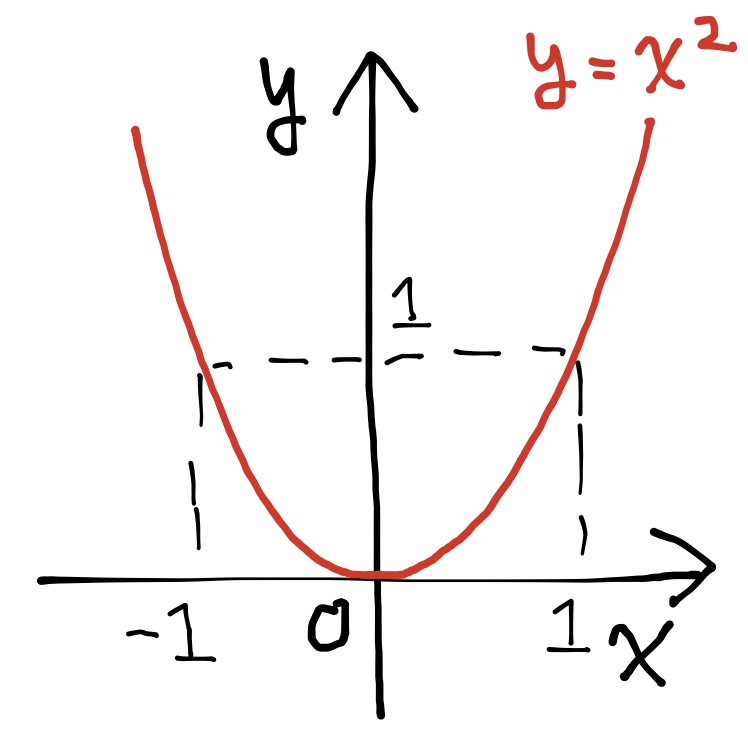
定義  自然数に対して実数を対応させる関数を数列という.

数列は, 普通, $\{a_n\}$とか, $$a_1,a_2,a_3,a_4,...$$ という形で書き表される.

• 1次関数(復習)

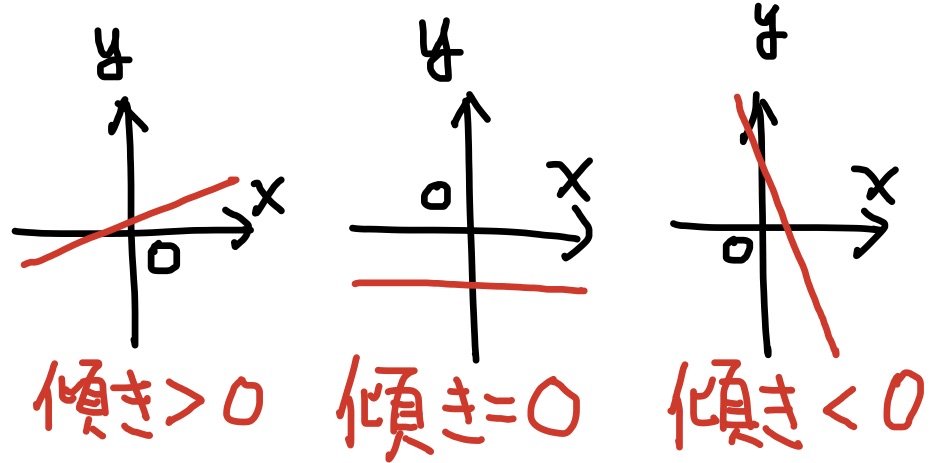
定数$a,b$に対し, $$y=ax+b$$で表される関数を1次関数と呼んだ. 1次関数のグラフは直線であり, 逆に直線は1次関数で表される(但し$y$軸と平行な直線は除く). $a$は直線の傾きを表す.



演習  1. 1次関数$y=2x$と$y=-x+2$のグラフを描きなさい.
2. 原点$O=(0,0)$を通り, 傾きが$3$の直線の式を求めなさい.
3. y軸と$y=-1$で交わる傾きが$-1$の直線の式を求めなさい.
4. 二点$(0,1),(2,0)$を通る直線の式を求めなさい.
5. 二点$(1,1),(2,4)$を通る直線の式を求めなさい.


• 2次関数(復習)

定数$a,b,c$に対し, $$y=ax^2+bx+c$$で表される関数を2次関数と呼んだ. 2次関数のグラフは放物線である. $a>0$のときグラフは下に凸であり, $a<0$のときグラフは上に凸である.



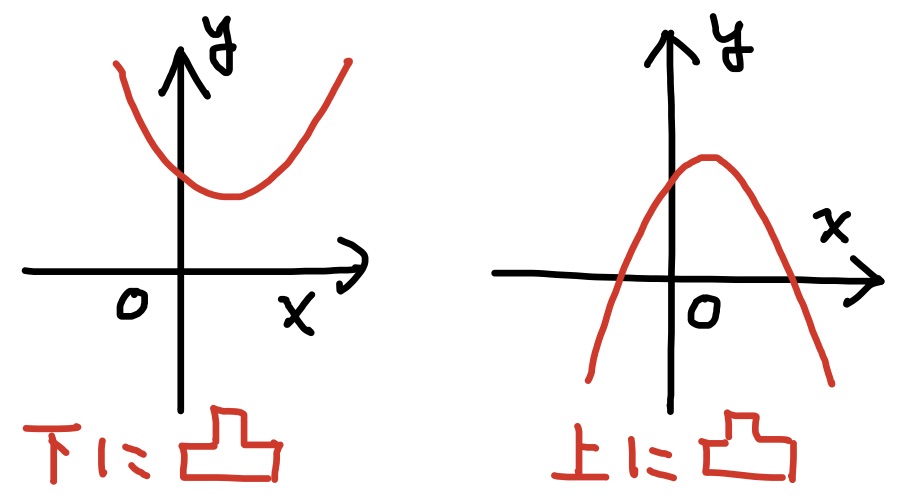
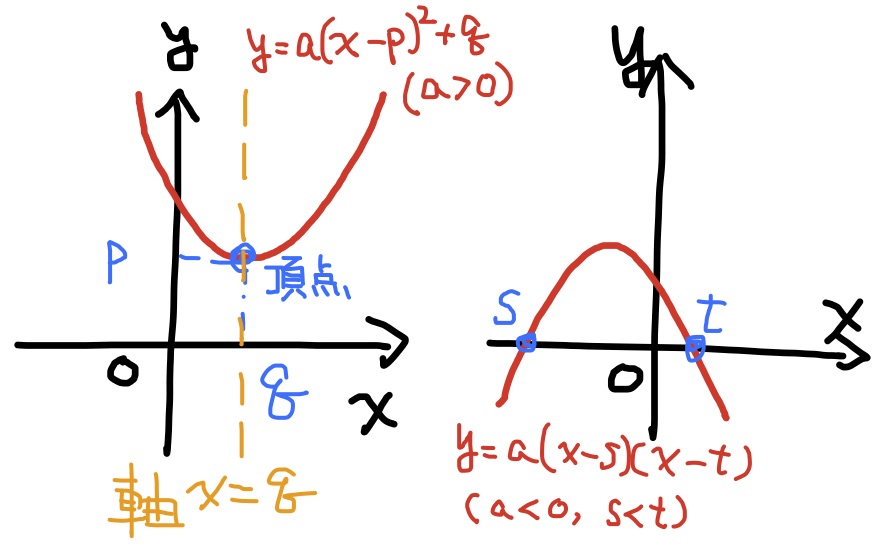
2次関数を表す式は上記の$y=ax^2+bx+c$ (これを一般形と呼ぶ)の他にも, $$y=a(x-p)^2+q\quad(標準形)\quad または\quad y=a(x-s)(x-t)\quad(分解形)$$ も良く現れる. 標準形から頂点$(p,q)$や軸$x=q$が分かるのでグラフを描きやすく, 分解形からは2次関数の根$x=s,t$, すなわち, x軸と放物線が交わる点を知ることができる.



一般形から標準形を求めることを平方完成という. 平方完成は $$ y=ax^2+bx+c =a\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2}{4a}+c $$ という公式から求めることができる.

分解形は因数分解して求めるほか, 2次方程式$ax^2+bx+c=0$の解の公式 $$x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}$$ を使って求めることもできる.

演習  1. 2次関数$y=x^2+4x+3$の標準形と分解形を求め, グラフを描きなさい.
2. 2次関数$y=-2x^2+4x-2$の標準形を求め, グラフを描きなさい.
3. 2次関数$y=3x^2+9$の分解形を求め, グラフを描きなさい.
4. 2次関数$y=2x^2+3x-1$の根を求めなさい.
5. 2次方程式$x^2-4x+1$の解を求めなさい.