関数$f(x)$について, 区間$I$上の点$u$での値$f(u)$が区間$I$上の最大値であるとは, $$f(x)\le f(u)$$ が区間$I$上の任意の点$x$で成り立つことを言う. 同様に, 関数$f(x)$について, 区間$I$上の点$b$での値$f(v)$が区間$I$上の最小値であるとは, $$f(x)\ge f(v)$$ が区間$I$上の任意の点$x$で成り立つことを言う.
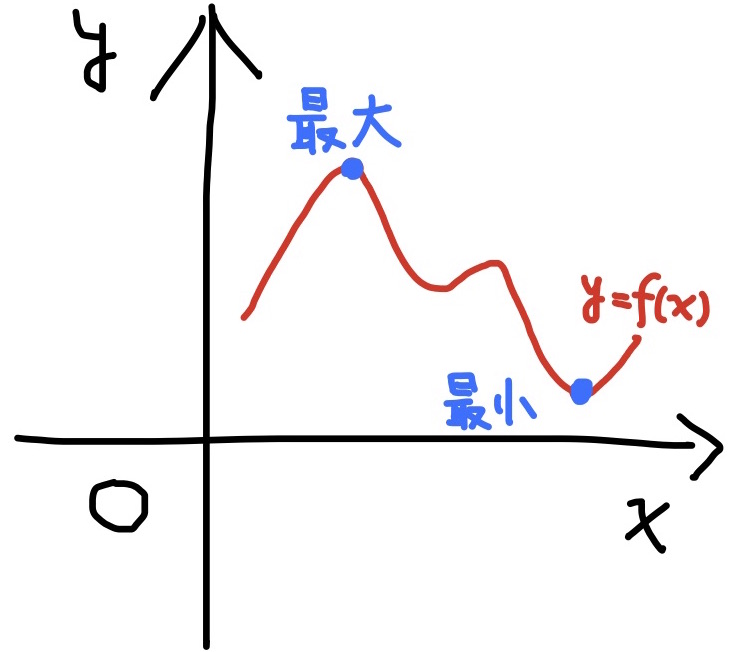
定理 閉区間$[a,b]$上で定義された連続関数$f(x)$は, この閉区間$[a,b]$上での最大値, 及び, 最小値を持つ.
証明
最大値の存在のみ示す(最小値の存在の証明も同様にできる).
数列$\{a_n\}_n,\{b_n\}_n$を
$$a=a_1\le a_2\le a_3\le\cdots\le b_3\le b_2\le b_1=b$$
かつ任意の$n$と任意の$x$ ($a\le x\le b$)について
$$f(x)\le f(u_x)\quad(a_n\le{}^\exists u_x\le b_n)\tag{1}$$
が成り立つように, 以下のように定義する.
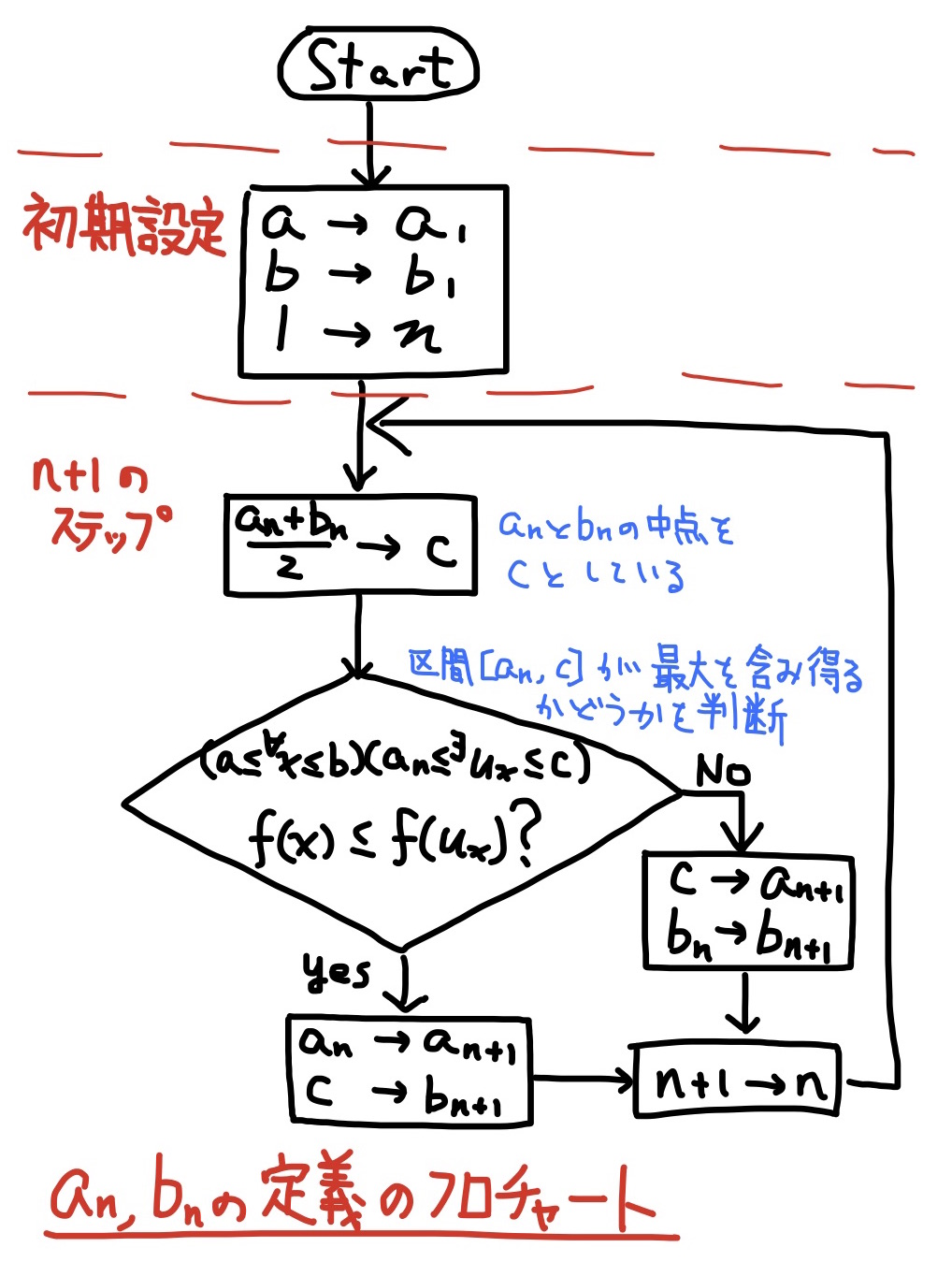
$a_1=a,b_1=b$とすれば, $n=1$のとき, 明らかに条件(1), つまり, 任意の$x$ ($a\le x\le b$)について
$$f(x)\le f(u_x)\quad(a_1\le{}^\exists u_x\le b_1)$$
が成り立つ($u_x=x$とおけばよい).
今, $a_n,b_n$が定まって, 任意の$x$ ($a\le x\le b$)について(1)が成り立つと仮定して,
$a_{n+1},b_{n+1}$を定める.
$c$を$a_n$と$b_n$の中点, すなわち, $c=\dfrac{a_n+b_n}{2}$とおけば,
$a_n<c<b_n$である.
このとき, $a_n,c$か$c,b_n$は条件(1)を満たす.
何故なら, そうでなければ, $x_1,x_2$ ($a\le x_1,x_2\le b$)が存在して,
$$f(x_1)> f(u)\quad(a_n\le{}^\forall u\le c),\qquad f(x_2)> f(u)\quad(c\le{}^\forall u\le b_n)\tag{2}$$
が成り立つ.
$x_1,x_2$のうち, $f(x_1)$,$f(x_2)$の値が大きくなる方を$x$と置けば,
(2)から,
$$f(x)> f(u)\quad(a_n\le{}^\forall u\le b_n)$$
が成り立つが, これは$a_n,b_n$が条件(1)を満たすことに反する.
以上で, $a_n,c$か$c,b_n$は条件(1)を満たすことが示された.
条件(1)を満たす方を片方選んで, それらを$a_{n+1},b_{n+1}$と定める.
以上で, 全ての自然数$n$について, 条件(1)が成り立つように$a_n,b_n$が定められた.
実数の完備性から
$$a=a_1\le a_2\le a_3\le...\le{}^\exists r\le...\le b_3\le b_2\le b_1=b$$
が成り立つ.
$f(r)$が区間$[a,b]$上で最大値となることを示そう.
区間$[a,b]$上の点$x$を任意に取る.
$$f(x)\le f(r)$$
であることを示したい.
各$n$について$a_n,b_n$は条件(1)を満たすから,
$$f(x)\le f(u_n)\quad(a_n\le u_n\le b_n)$$
となるように$\{u_n\}_n$を選ぶことができる.
$a_n,b_n\to r$ ($n\to\infty$)であるから,
挟み込みの原理から$u_n\to r$ ($n\to\infty$)である.
不等式$f(x)\le f(u_n)$の極限を考えると,
$$f(x)=\lim_{n\to\infty}f(x)\le\lim_{n\to\infty}f(u_n)
\underset{fは連続}{=}f(r)$$
となり, $f(x)\le f(r)$が分かる.
定義 関数$f(x)$について, 関数$f(x)$の局所的な最大値を$f(x)$の極大(値)といい, 局所的な最小値を$f(x)$の極小(値)という. また, 極大/極小をまとめて$f(x)$の極値という.
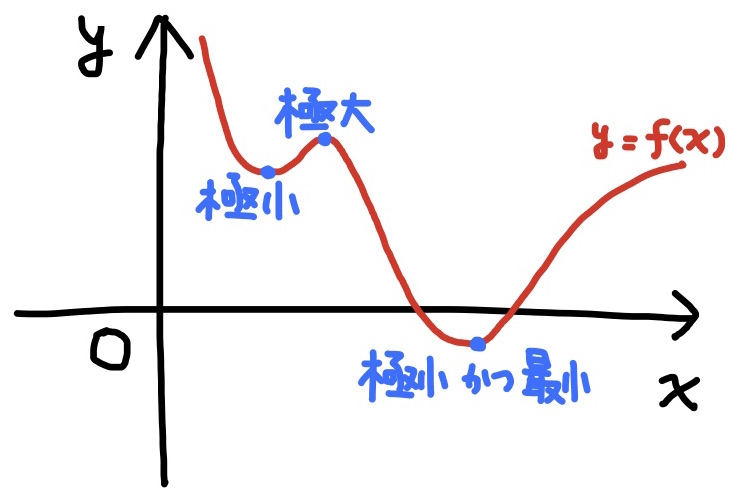
言葉を足せば, $f(x)$の局所的な最大値とは, ある区間$(a,b)$に関数$f(x)$を制限すると, その範囲内で最大となるような値のことを意味する.
定理 極値での微分は$0$である. すなわち, 微分可能関数$y=f(x)$が$x=a$で極値と取るとき, $$f^\prime(a)=0$$が成り立つ.
証明 $$\dfrac{f(v+h)-f(v)}{h} \begin{cases} \le 0 & h>0\mbox{のとき}\\ \ge 0 & h<0\mbox{のとき} \end{cases}$$ が分かる. $h$を$0$に近づける極限を考えると左辺の分数は$f^\prime(v)$に近づくから, $$f^\prime(v)=\lim_{h\to +0}\dfrac{f(v+h)-f(v)}{h}\le 0\le\lim_{h\to -0}\dfrac{f(v+h)-f(v)}{h}=f^\prime(v)$$ を得る. よって, $f^\prime(v)\le 0\le f^\prime(v)$, 従って, $f^\prime(v)=0$が成り立つ. 以上で定理の(1)が$c=v$として成り立つことが分かった.
定理 閉区間$[a,b]$上の連続関数$f(x)$は $f(a)=f(b)$のとき, 開区間$(a,b)$で極値を持つ. 従って, $$f^\prime(x)=0\quad(a<{}^\exists x< b)$$ が成り立つ.
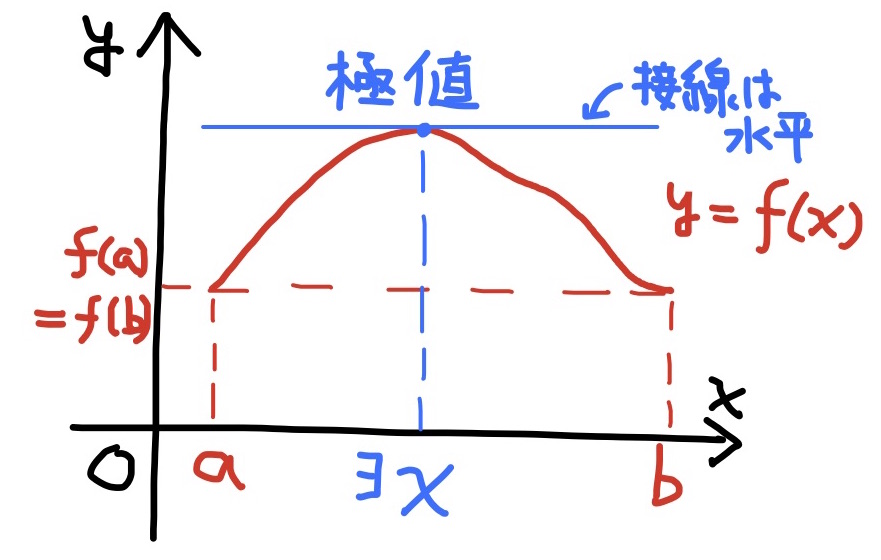
証明 関数$f(x)$が定数関数であれば, $a$から$b$の間のどの$x$でも極大かつ極小なので良い. そうでないときを考える. 最大・最小の原理から閉区間$[a,b]$で関数$f(x)$は最大値$f(u)$と最小値$f(v)$を持つ. 今, 関数$f(x)$は定数でないと仮定しているので, $x=u$か$x=v$のどちらかの値$f(x)$は, $f(a)(=f(b))$とは異なる値となっている. そのような$x$について, $x\ne a,b$であるから, $$a<x<b$$ である. また, 最大であれば極大, 最小であれば極小であるから, $f(x)$は極値である.
