but to myself I seem to have been only like a boy playing on the sea-shore,
and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary,
whilst the great ocean of truth lay all undiscovered before me.


日大工 総合教育 樋口幸治郎
| ホーム | 教室 | 研究室 |
|---|---|---|
| 工科系数学I及び演習 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
I do not know what I may appear to the world,
but to myself I seem to have been only like a boy playing on the sea-shore,
and diverting myself in now and then finding a smoother pebble or a prettier shell than ordinary,
whilst the great ocean of truth lay all undiscovered before me.

--- Isaac Newton
アイザック・ニュートンの晩年の言葉
微分の意味を学び, 微分の線形性を学ぶ. (教科書p3-10)
定義 変数$x$が値$x=a$から別の値$x=b$に変化するとき, その差$b-a$を $$\varDelta x$$ で表し. これを$x$の増分という.
関数$y=f(x)$について, 独立変数$x$の$x=a$から$x=b$への変化の増分$\varDelta x$に応じて, 従属変数$y$の$y=f(a)$から$y=f(b)$への変化の増分$\varDelta y$も決まる. このとき二つの増分の割合 $$\dfrac{\varDelta y}{\varDelta x} =\dfrac{f(a+\varDelta x)-f(a)}{\varDelta x} =\dfrac{f(b)-f(a)}{b-a} $$ を, $x$が$a$から$b$に変化するときの関数$y=f(x)$の平均変化率という.
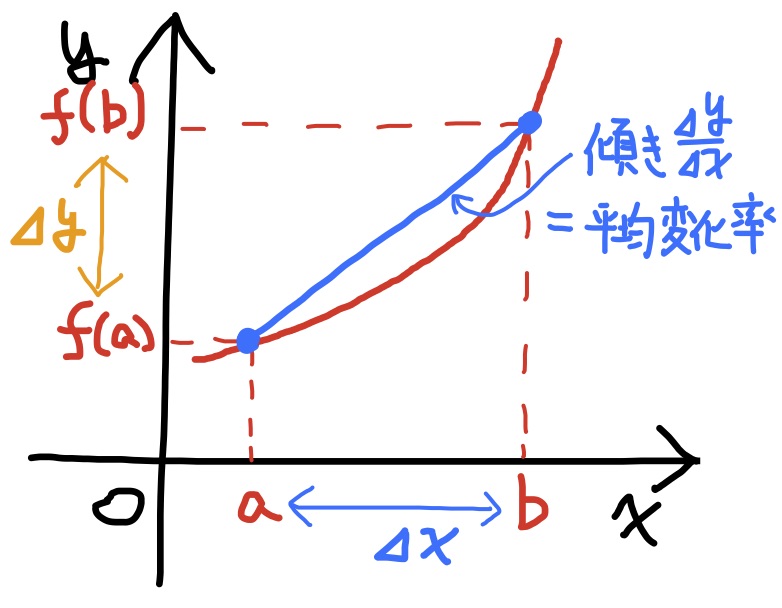
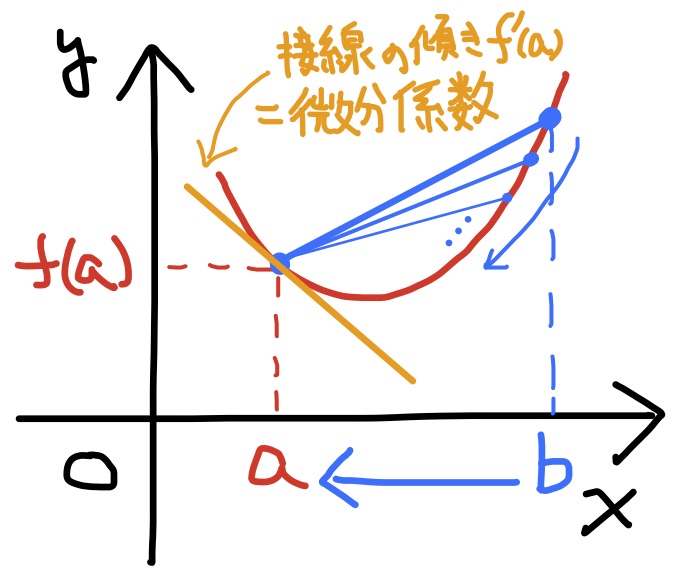
関数$y=f(x)$の$x=a$での微分とは, $x=a$での関数$f(x)$の変化率, 或いは, 言わば瞬間の変化率を意味する. これは, 平均変化率の極限として表現することができる.
定義 関数$y=f(x)$について, 極限 $$\lim_{\varDelta x\to 0}\dfrac{\varDelta y}{\varDelta x} =\lim_{\varDelta x\to 0}\dfrac{f(a+\varDelta x)-f(a)}{\varDelta x} =\lim_{b\to a}\dfrac{f(b)-f(a)}{b-a} $$ が収束するとき, 関数$y=f(x)$は$x=a$で微分可能であるといい, その極限値を$f^\prime(a)$や$\left.\dfrac{dy}{dx}\right|_{x=a}$で書き表し, これを関数$y=f(x)$の$x=a$での微分, 又は, 微分係数という.
定義域上のどの点$x=a$でも微分可能である関数を微分可能関数といい, 区間$I$上のどの点$x=a$でも微分可能であるときには, $I$上で微分可能という.
微分可能関数$y=f(x)$について, 「$a\mapsto f^\prime(a)$」という対応が定める関数を, 関数$y=f(x)$の導関数, 又は, 微分という. (「微分」は多義語, つまり, 微分係数や導関数を意味するときがあり注意を要する.) $f(x)$の導関数を $$y^\prime,\quad f^\prime,\quad f^\prime(x),\quad \dfrac{dy}{dx},\quad \dfrac{df}{dx},\quad \dfrac{d}{dx}f(x)$$ などと書く. 微分の定義から $$f^\prime(x)=\dfrac{dy}{dx}=\lim_{\varDelta x\to 0}\dfrac{\varDelta y}{\varDelta x} =\lim_{\varDelta x\to 0}\dfrac{f(x+\varDelta x)-f(x)}{\varDelta x} =\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h} =\lim_{x_1\to x}\dfrac{f(x_1)-f(x)}{x_1-x}$$ などが成り立つが, どれも良く使う. また, $$\left.f^\prime(x)\right|_{x=a}=f^\prime(a)$$ である. つまり, 導関数$f^\prime(x)$を求めておけば, 微分係数$f^\prime(a)$は$x=a$を代入すれば得られる.
例
1. 1次関数$y=x$の導関数は
$$\displaystyle y^\prime=(x)^\prime=
\lim_{h\to 0}\dfrac{x+h -x}{h}=
\lim_{h\to 0}\dfrac{h}{h}=
\lim_{h\to 0}1=
1$$である.
2. 2次関数$y=x^2$の導関数は
$$\displaystyle y^\prime=\big(x^2\big)^\prime=
\lim_{h\to 0}\dfrac{(x+h)^2 -x^2}{h}=
\lim_{h\to 0}\dfrac{2xh+(h)^2}{h}=
\lim_{h\to 0}\big(2x+h\big)=
2x$$である.
3. 関数$y=\dfrac{1}{x}$の導関数は
$$\displaystyle y^\prime
=\left(\dfrac{1}{x}\right)^\prime
=\lim_{h\to 0}\dfrac{\dfrac{1}{x+h}-\dfrac{1}{x}}{h}
=\lim_{h\to 0}\dfrac{\left(\dfrac{x-(x+h)}{x(x+h)}\right)}{h}
=\lim_{h\to 0}\dfrac{-h}{hx(x+h)}
=\lim_{h\to 0}\dfrac{-1}{x(x+h)}
=-\dfrac{1}{x^2}
$$である.
4. 定数関数$y=k$ ($k$は定数) の導関数は
$$\displaystyle y^\prime=\big(k\big)^\prime=
\lim_{h\to 0}\dfrac{k-k}{h}=
\lim_{h\to 0}0=
0$$である.
定理 微分は線形性を持つ(定数倍や和・差を保つ). つまり, 微分可能関数$f(x),g(x)$に対し, $kf(x)$ ($k$は定数), $f(x)\pm g(x)$も微分可能で $$\Big(kf(x)\Big)^\prime =kf^\prime(x),\qquad \big(f(x)\pm g(x)\big)^\prime =f^\prime(x)\pm g^\prime(x)$$ が成り立つ.
証明 それぞれ $$\displaystyle\big(k f(x)\big)^\prime \underset{\because 微分の定義}{=} \displaystyle\lim_{h\to 0}\dfrac{kf(x+h)-kf(x)}{h} =\displaystyle\lim_{h\to 0}k\dfrac{f(x+h)-f(x)}{h} \underset{\because \lim は定数倍を保つ}{=} \displaystyle k\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h} \underset{\because 微分の定義}{=} \displaystyle kf^\prime(x)$$ $$\big(f(x)\pm g(x)\big)^\prime \underset{\because 微分の定義}{=} \displaystyle\lim_{h\to 0}\dfrac{\big(f(x+h)\pm g(x+h)\big)-\big(f(x)\pm g(x)\big)}{h} \underset{f,g毎に纏め}{=} \displaystyle\lim_{h\to 0}\left(\dfrac{f(x+h)-f(x)}{h}\pm\dfrac{g(x+h)-g(x)}{h}\right)$$ $$\underset{\because \lim は\pm を保つ}{=}\displaystyle\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}\pm\lim_{h\to 0}\dfrac{g(x+h)-g(x)}{h} \underset{\because 微分の定義}{=}f^\prime(x)\pm g^\prime(x)$$ より得られる.
例
$\big(2x-5\big)^\prime=2(x)^\prime-(5)^\prime=2$
$\big(-3x^2+5x+1\big)^\prime=-3(x^2)^\prime+5(x)^\prime+(1)^\prime=6x+5$
微分と連続性の関係や合成関数の微分公式, 積・商の微分公式を学ぶ. (教科書p34-40)
定理 関数$f(x)$について, $$f(x)はx=aで微分可能\quad\Longrightarrow\quad f(x)はx=aで連続$$ が成り立つ. 故, 微分可能関数は連続関数である.
証明 $\displaystyle\lim_{b\to a}f(b)=f(a)$を示せばよい. $\displaystyle\lim_{b\to a}f(b)$ $\underset{一見無駄なものを付加}{=} \displaystyle\lim_{b\to a}\left(\dfrac{f(b)-f(a)}{b-a}\cdot(b-a)+f(a)\right)$ $\underset{\because \lim は四則演算を保つ}{=} \displaystyle\lim_{b\to a}\dfrac{f(b)-f(a)}{b-a}\cdot\lim_{b\to a}(b-a)+\lim_{b\to a}f(a)$ $\underset{\because \lim を計算}{=} f^\prime(a)\cdot(a-a)+f(a)$ $=f(a)$ が成り立つ.
定理 $f(t)$は微分可能であるとする. このとき, 連続関数$g(x)$について $$ g(x)が微分可能\quad\iff\quad f(g(x))は微分可能 $$ であって(但し"$\Longleftarrow$"では$f^\prime(g(x))\ne 0$を仮定), さらに, $$\Big(f(g(x))\Big)^\prime =\left.f^\prime(t)\right|_{t=g(x)}\cdot g^\prime(x) =f^\prime(g(x))g^\prime(x)$$ が成り立つ. (これを
証明 実数$h\ne 0$に対して, $k$を $$k=\begin{cases} g(x+h)-g(x) & g(x+h)-g(x)\ne 0のとき\\ h & g(x+h)-g(x)= 0のとき \end{cases}$$ と定めると, $k\ne 0$であり, また関数$g(x)$は連続だから$k\to 0$ ($h\to 0$)である. また, 等式 $$\dfrac{f(g(x+h))-f(g(x))}{h}=\dfrac{f(g(x)+k)-f(g(x))}{k}\cdot\dfrac{g(x+h)-g(x)}{h}$$ が成り立つが, この等式に対し$h\to 0$の極限を考えると, $k\to 0$ ($k\ne 0$)なので右辺の第一の分数は$f^\prime(g(x))$となるので, $$\lim_{h\to 0}\dfrac{f(g(x+h))-f(g(x))}{h}=f^\prime(g(x))\cdot\lim_{h\to 0}\dfrac{g(x+h)-g(x)}{h}$$ を得る. 左辺/右辺の極限は, それぞれ$(f(g(x)))^\prime,g^\prime(x)$のことである. 従って, $g^\prime(x)$の値が存在すれば$(f(g(x)))^\prime$の値も存在し, $$\big(f(g(x))\big)^\prime=f^\prime(g(x))g^\prime(x)$$ が成り立つ. $f^\prime(g(x))\ne 0$の仮定のもとでは, 逆に, $(f(g(x)))^\prime$の値が存在すれば$g^\prime(x)$の値も存在し, 同様に上の式が成り立つ.
定理 $\Big(f(x)g(x)\Big)^\prime=f^\prime(x)g(x)+f(x)g^\prime(x)$
証明 $$ \begin{align} \Big(f(x)g(x)\Big)^\prime &=\lim_{h\to 0}\dfrac{f(x+h)g(x+h)-f(x)g(x)}{h} =\lim_{h\to 0}\dfrac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h}\\ &=\left(\lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}\cdot g(x+h)+f(x)\cdot \dfrac{g(x+h)-g(x)}{h}\right)\\ &\underset{\because limは四則演算を保つ}{=} \lim_{h\to 0}\dfrac{f(x+h)-f(x)}{h}\cdot \lim_{h\to 0}g(x+h)+f(x)\lim_{h\to 0}{g(x+h)-g(x)}{h}\\ &\underset{\because 微分の定義}{=} f^\prime(x)\cdot \lim_{h\to 0}g(x+h)+f(x)g^\prime(x)\\ &\underset{\because 連続性}{=} f^\prime(x)g(x)+f(x)g^\prime(x) \end{align} $$
系 $\left(\dfrac{1}{g(x)}\right)^\prime=-\dfrac{g^\prime(x)}{g(x)^2},$ $\left(\dfrac{f(x)}{g(x)}\right)^\prime=\dfrac{f^\prime(x)g(x)-f(x)g^\prime(x)}{g(x)^2}$ (但し$g(x)\ne 0$)
証明 二つの等式 $$g(x)\cdot\dfrac{1}{g(x)}=1,\qquad g(x)\cdot\dfrac{f(x)}{g(x)}=f(x)$$ において両辺を微分して, それぞれの左辺は積の微分公式を使えば, $$g^\prime(x)\cdot\dfrac{1}{g(x)}+g(x)\cdot\left(\dfrac{1}{g(x)}\right)^\prime=0,\qquad g^\prime(x)\cdot\dfrac{f(x)}{g(x)}+g(x)\cdot\left(\dfrac{f(x)}{g(x)}\right)^\prime=f^\prime(x)$$ を得る. それぞれの両辺を$g(x)$で割り, 左辺の第一項を右辺に移行して整理すれば, $$\left(\dfrac{1}{g(x)}\right)^\prime=-\dfrac{g^\prime(x)}{g(x)^2},\qquad \left(\dfrac{f(x)}{g(x)}\right)^\prime=\dfrac{f^\prime(x)g(x)-f(x)g^\prime(x)}{g(x)^2}$$ を得る.
課題 教科書p34の問1, p36の問2, p37の問5,6 のうち, 無理関数を含まない問題の中から8問以上を選んで解きなさい.