国勢調査によって, 日本人の全体の人口や, 年齢別の人口が調べられている. 今, 無作為に一人の日本人を選び出すとしよう(例えば日本のどこかの道を歩いてみて, 最初に出会った人). この人の年齢が$25$歳である(という事象の)確率はどの程度であろうか. $25$歳である人口$f_{25}$を日本全体の人口$N$で割った$\dfrac{f_{25}}{N}$と考えられるであろう. これは$25$歳の日本人の集合が, 日本人全体の集合の中で占める割合である. このように, 確率は, 何かの全体集合(=標本空間)の一部の集合(=事象)に対して割り当てられている.
定義 集合とはモノの集まりのことである.
- 集合の表記
集合は$$\{1,2,3,4,5\}$$のようにその要素を書き尽くして表す記法(外延的記法)と, $$\{n\mid nは5以下の正の整数\}$$のようにその要素の持つ性質を記述する記法(内包的記法)とがある. 集合$A$の内包的記法$$A=\{x\mid P(x)\}$$で使われる性質P(x)と集合Aはしばしば同一視される.
モノ$x$が集合$A$の要素であることを $$x\in A$$ と書く. 要素でないことは $$x\not\in A$$ と書く.
定義 要素を一つも持たない集合を空集合という. 空集合を $$\emptyset,\qquad \{\}$$ などと書く.
定義 集合$A$が集合$B$の一部となっているとき, 言い換えると, $A$の任意の要素は$B$の要素であるとき, $A$は$B$の部分集合といい, $$A\subset B$$ と書く.
例えば$\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}$である. 但し, $\mathbb{N},\mathbb{Z},\mathbb{Q},\mathbb{R},\mathbb{C}$はそれぞれ自然数(natural number)全体, 整数(integer)全体, 有理数(rational number)全体, 実数(real number)全体, 複素数(complex number)全体の集合を表す.
定義 標本空間とは集合のことである. 標本空間は$\Omega$, $U$で表すことが多い.
標本空間は何かの実験や観測(これらを試行という)での有り得る結果の全体と考える.
定義 標本空間$\Omega$の部分集合を事象という.
標本空間の要素$x\in\Omega$が事象$A$の要素であれば, 実験や観測の結果$x$として$A$という事象が起こった, と考える.
標本空間$\Omega$, 空集合$\emptyset$はそれぞれ全事象, 空事象ともいう.
標本空間$\Omega$での事象はベン図を用いて議論すると分かりやすくなることがある.
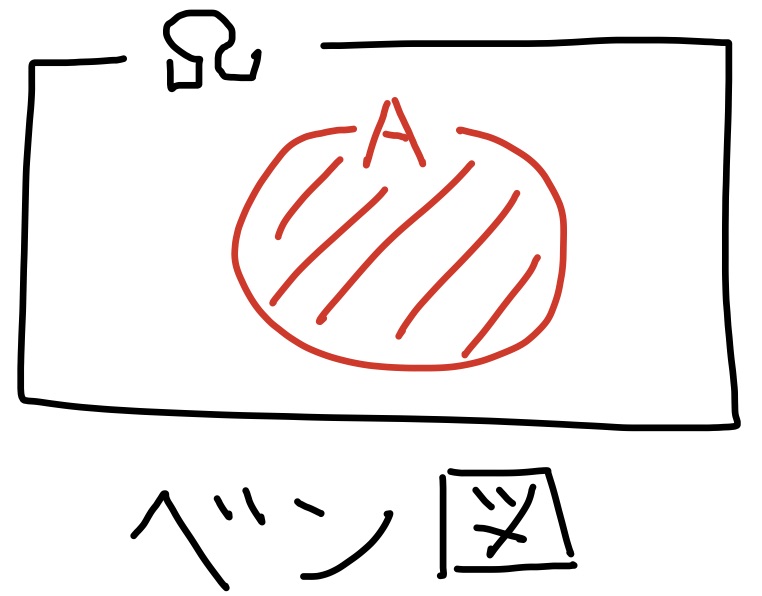
定義
標本空間$\Omega$での事象$A,B$について,
和事象$A\cup B$・・・性質「$A$または$B$ (つまり$x\in A$ or $x\in B$)」が定める事象
積事象$A\cap B$・・・性質「$A$かつ$B$ (つまり$x\in A$ and $x\in B$)」が定める事象
余事象$A^{\rm c}$・・・・・性質「$A$でない (つまり$x\not\in A$)」が定める事象
差事象$A-B$・・・性質「$B$を除く$A$ (つまり$x\in A$ and $x\not\in B$)」が定める事象
と定める.
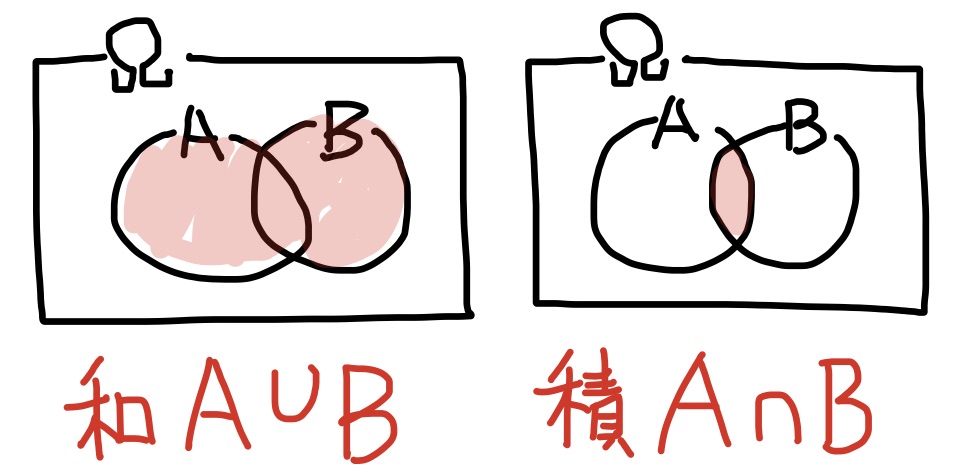
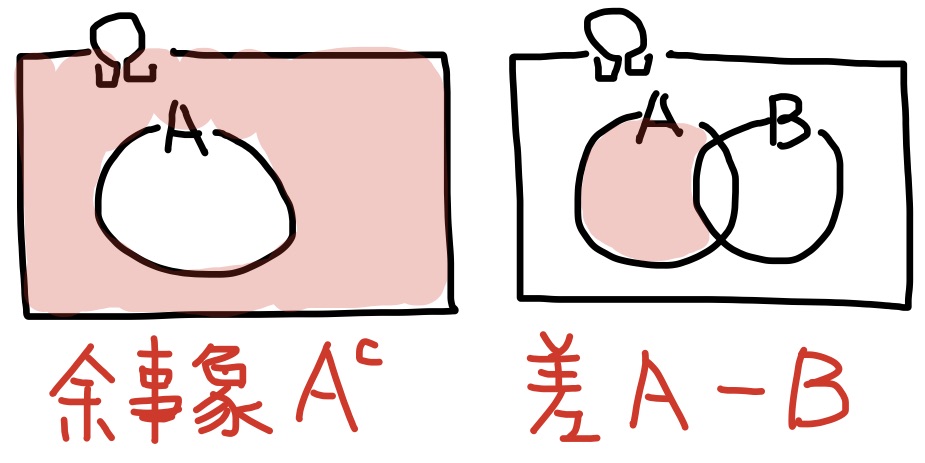
演習 色々な事象をベン図で描いてみよう.
定義
標本空間$\Omega$での事象$A_1,A_2,A_3,A_4,\cdots$について,
可算無限和$\displaystyle \bigcup_{i=1}^\infty A_i$・・性質「$x\in A_1$ or $x\in A_2$ or $x\in A_3$ or ...」が定める事象
(性質「$x\in A_i$ for some $i\in\mathbb{N}$」の事象とも言える)
可算無限積$\displaystyle \bigcap_{i=1}^\infty A_i$・・性質「$x\in A_1$ and $x\in A_2$ and $x\in A_3$ and ...」が定める事象
(性質「$x\in A_i$ for all $i\in\mathbb{N}$」の事象とも言える)
と定める.
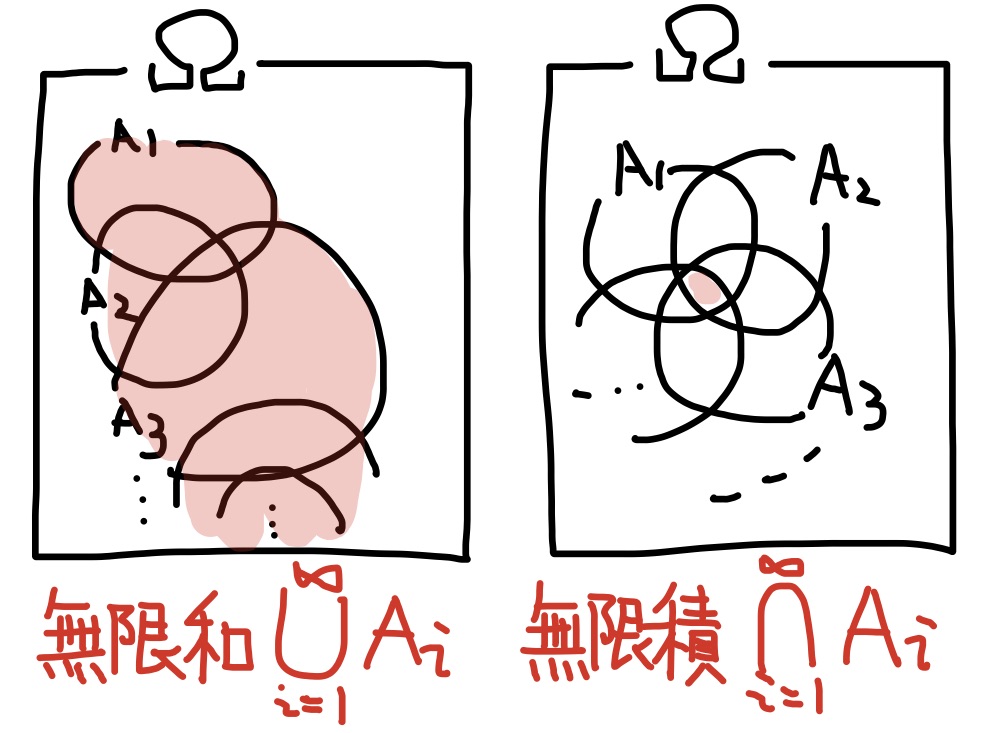
定義
標本空間$\Omega$での事象$A,B$について,
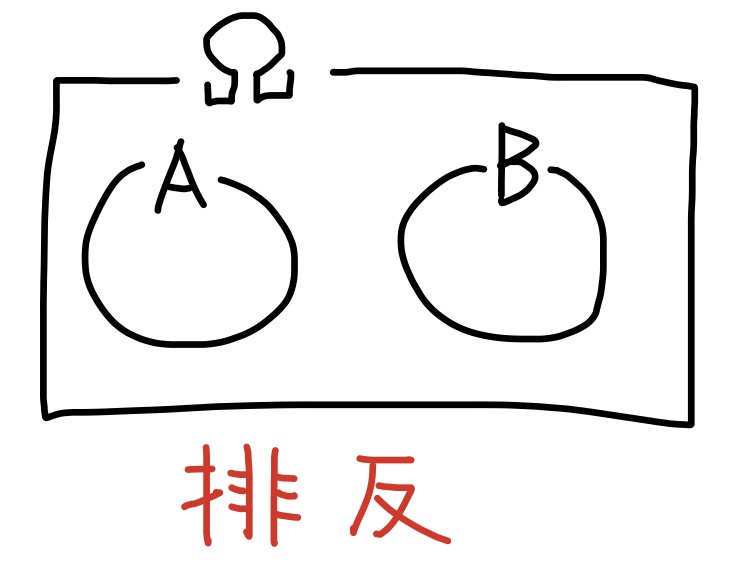
$A\cap B=\emptyset$のとき, $A$と$B$は互いに排反とか, 互いに素という.

定義
標本空間$\Omega$上の確率$P(\cdot)$とは, 以下の条件を満たす$\Omega$の事象(の一部)に対して実数を割り当てる関数のことである:
(P0) 関数$P(\cdot)$が値を持つ事象の(可算無限)和・(可算無限)積・余・差事象もまた値を持つ.
(P1) $0\le P(A)\le 1\quad$(事象$A$に対し値$P(A)$が定まっているとき)
(P2) $P(\Omega)=1$
(P3) 完全加法性 $\displaystyle P\left(\bigcup_{i=1}^\infty A_i\right)=\sum_{i=1}^\infty P(A_i)\quad$(事象$A_1,A_2,A_3,\cdots$は互いに排反で, 値$P(A_1),P(A_2),P(A_3)$が全て定まっているとき)
標本空間$\Omega$上の確率$P$について, 確率の定義から以下の確率が持つべき自然な性質が導かれる.
- $P(\emptyset)=0$
- $A,B$が互いに排反なら, $P(A\cup B)=P(A)+P(B)$
- $P(A^{\rm c})=1 - P(A)$
- $A\subset B\Longrightarrow P(A)\le P(B)$
証明 $\emptyset=\bigcup_{i=1}^\infty$であり, $\emptyset,\emptyset,\emptyset,...$は互いに排反だから, 両辺の確率は $$P(\emptyset)=P\left(\bigcup_{i=1}^\infty\emptyset\right) \underset{(P3)}{=}\sum_{i=1}^\infty P(\emptyset)=P(\emptyset)+P(\emptyset)+...$$ である. 条件(P1)より$0\le P(\emptyset)\le 1$であるが, 上の等式が成り立つためには$P(\emptyset)=0$でなければならない.
証明 $A,B,\emptyset,\emptyset,\emptyset,...$は互いに排反だが, この和集合は$A\cup B$なので, 完全加法性P3から $$P(A\cup B)=P(A)+P(B)+P(\emptyset)+P(\emptyset)+...=P(A)+P(B)+0+0+...=P(A)+P(B)$$ が得られる.
証明 $A,A^{\rm c}$は互いに排反で, 和集合$A\cup A^{\rm c}=\Omega$だから $$1\underset{(P2)}{=}P(\Omega)=P(A\cup A^{\rm c})=P(A)+P(A^{\rm c})$$ が得られる. 移行すれば求める等式が得られる.
証明 $A,B-A$は互いに排反で, 和集合$A\cup(B-A)=B$だから $$P(B)=P(A\cup(B-A))=P(A)+P(B-A)\underset{(P1)}{\ge} P(A)$$ が得られる.
