今回学ぶ微積分学の基本公式のために, 差の記号を導入し, 幾つかの性質を見ておこう.
定義 関数$F(x)$について, $$\Big[F(x)\Big]^b_a=F(b)-F(a)$$ と定める.
定理 $$\Big[F(x)\pm G(x)\Big]^b_a=\Big[F(x)\Big]^b_a\pm\Big[G(x)\Big]^b_a,\qquad \Big[kF(x)\Big]^b_a=k\Big[F(x)\Big]^b_a\quad(kは定数)$$ $$\Big[F(x)\Big]^b_a=\Big[F(x)\Big]^c_a+\Big[F(x)\Big]^b_c$$ $$\Big[F(x)+C\Big]^b_a=\Big[F(x)\Big]^b_a\quad(Cは定数)$$
証明. $$\begin{align} \Big[F(x)\pm G(x)\Big]^b_a =(F(b)\pm G(b))-(F(a)\pm G(a))\\ =(F(b)-F(a))\pm(G(b)- G(a)) =\Big[F(x)\Big]^b_a\pm\Big[G(x)\Big]^b_a \end{align}$$ $$\begin{align} \Big[kF(x)\Big]^b_a =kF(b)-kF(a) =k(F(b)-F(a)) =k\Big[F(x)\Big]^b_a \end{align}$$ $$\begin{align} \Big[F(x)\Big]^c_a+\Big[F(x)\Big]^b_c =(F(c)-F(a))+(F(b)-F(c)) =F(b)-F(a) =\Big[F(x)\Big]^b_a \end{align}$$ $$\begin{align} \Big[F(x)+C\Big]^b_a =(F(b)+C)-(F(a)+C) =F(b)-F(a) =\Big[F(x)\Big]^b_a \end{align}$$
定義 $a<b$とする. 関数$y=f(x)$について, $y=f(x)$のグラフと, 垂線$x=a,x=b$と$x$軸で囲まれる図形の面積を $$\int^b_af(x)dx$$ で表し, これを $$f(x)のaからbまでの定積分$$ という. 但し, $x$軸より上は正の面積, 下は負の面積とする.
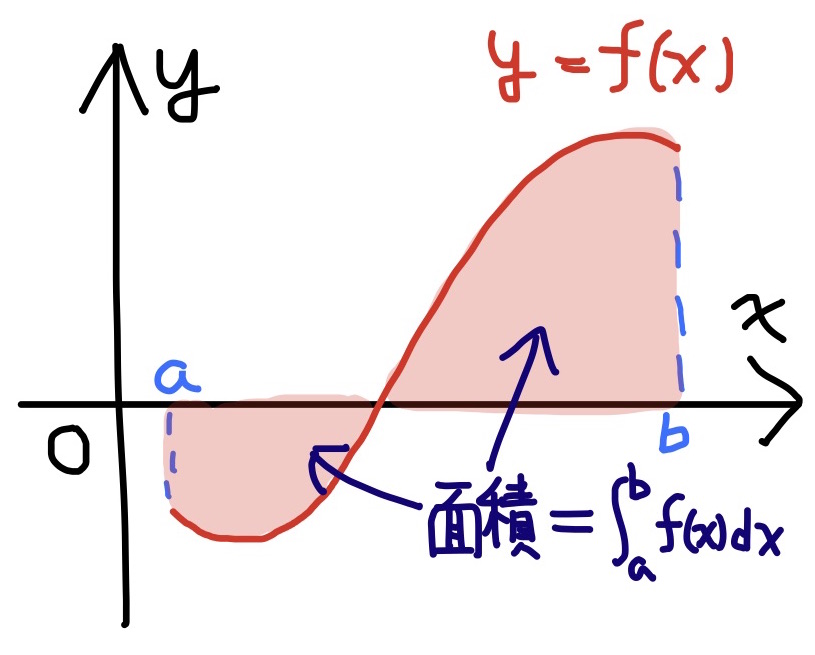
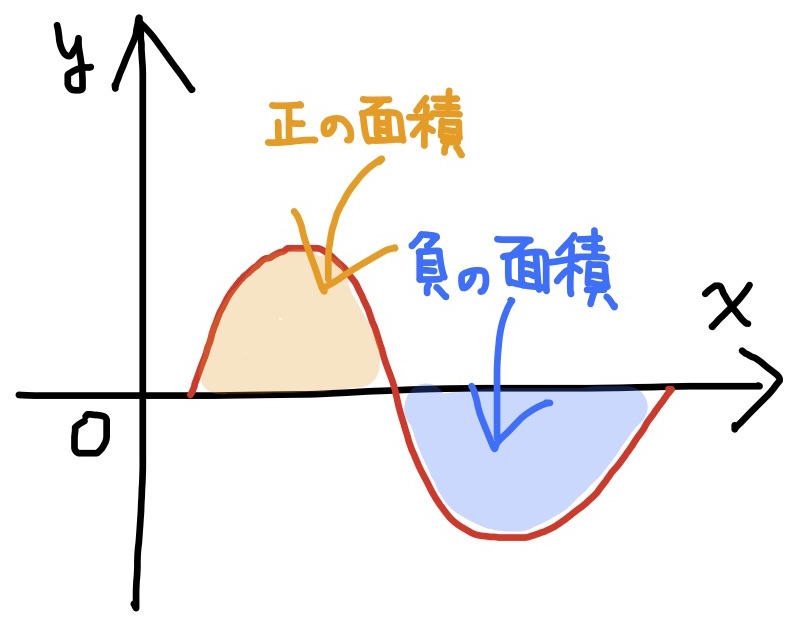
$a<b$でないときも定積分を以下のように定める. $$a>b\ ならば\ \int^b_af(x)dx=-\int^a_bf(x)dx$$ $$a=b\ ならば\ \int^b_af(x)dx=0$$
上記のように $$定積分\int^b_af(x)dx = aからbまでのf(x)の面積$$ と定義した. $f(x)$が直線のように単純であれば, その面積を求めることは難しくはないだろう. もっと複雑な関数の場合はどうだろうか? 面積をどのように求めれば良いだろうか? また, そもそも面積とは何か?
数学では, しばしば, $$よく分かっている単純なモノの極限として, 複雑なモノを取り扱う$$ というアイディアを用いる. このアイディアを用いて, $$複雑な図形を長方形の組み合わせで近似$$ することを考え, $$図形の面積を長方形の組み合わせの図形の面積の極限$$ と定義することができる. このアイディアに基づいた定積分のより厳密な定義は教科書p146-147にある.
(微積分学の)基本公式は, 一見関係のなさそうな不定積分(=微分の逆)と定積分(=面積)を結びつける非常に重要な公式であり, これにより, 定積分の値や性質が, 不定積分を用いて調べることができるようになる. $$微分の性質\quad \overset{「約分」+「移行」}{\Longrightarrow}\quad 不定積分の性質\quad \overset{基本公式}{\Longrightarrow}\quad 定積分の性質$$
(微積分学の)基本公式(p152の[VII]) $$\int^b_af(x)dx=\left[\int f(x)dx\right]^b_a$$ (時間の制約上, 講義では基本公式の証明(教科書p149-152を見よ)を行わない.)
定積分の計算では積分定数は不要であることを説明しよう. 差の記号の性質 $$\Big[F(x)+C\Big]^b_a=\Big[F(x)\Big]^b_a\quad(Cは定数)$$ から, 不定積分の差$\displaystyle\left[\int f(x)dx\right]^b_a$の計算は, 不定積分$\displaystyle\int f(x)dx$の一般解$F(x)+C$を考えるまでもなく, 一つの特殊解$F(x)$で計算すれば良い. つまり, $f(x)$の原始関数$F(x)$について, $$\left[\int f(x)dx\right]^b_a=\Big[F(x)\Big]^b_a$$ となる. だから, 定積分を基本公式を使って計算するとき, 付随する不定積分の計算で積分定数は不要である.
計算例. $$\begin{align} &\int^2_1xdx\\ \underset{基本公式}{=}&\left[\dfrac{1}{2}x^2\right]^2_1\qquad(積分定数は不要!)\\ =&\dfrac{1}{2}\cdot 2^2-\dfrac{1}{2}\cdot 1^2\\ =&\dfrac{3}{2} \end{align}$$
基本公式により, 不定積分の性質が定積分の性質として輸入される.
定理 $$\int^b_a(f(x)\pm g(x))dx=\int^b_a f(x)dx\pm\int^b_a g(x)dx,\qquad \int^b_a(kf(x))dx=k\int^b_a f(x)dx\quad(kは定数)$$
証明. $$\begin{align} &\int^b_a(f(x)\pm g(x))dx\\ \underset{基本公式}{=}&\left[\int (f(x)\pm g(x))dx\right]^b_a\\ \underset{不定積分の性質}{=}&\left[\int f(x)dx\pm\int g(x)dx\right]^b_a\\ \underset{差の記号の性質}{=}&\left[\int f(x)dx\right]^b_a\pm\left[\int g(x)dx\right]^b_a\\ \underset{基本公式}{=}&\int^b_a f(x)dx\pm\int^b_a g(x)dx \end{align}$$ $$\begin{align} &\int^b_a(kf(x))dx\\ \underset{基本公式}{=}&\left[\int(kf(x))dx\right]^b_a\\ \underset{不定積分の性質}{=}&\left[k\int f(x)dx\right]^b_a\\ \underset{差の記号の性質}{=}&k\left[\int f(x)dx\right]^b_a\\ \underset{基本公式}{=}&k\int^b_a f(x)dx \end{align}$$
定理 $$\int^b_af(x)dx=\int^c_a f(x)dx+\int^b_c f(x)dx$$
証明. $$\begin{align} &\int^b_af(x)dx\\ \underset{基本公式}{=}&\left[\int f(x)dx\right]^b_a\\ \underset{差の記号の性質}{=}&\left[\int f(x)dx\right]^c_a+\left[\int g(x)dx\right]^b_c\\ \underset{基本公式}{=}&\int^c_a f(x)dx+\int^b_c f(x)dx \end{align}$$
- 例題1(p16)
(1) $\displaystyle\int^2_04x^3dx=?$ (2) $\displaystyle\int^1_{-1}(3x^2-x+1)dx=?$
答. (1)
$$\begin{align}
&\int^2_04x^3dx\\
\underset{基本公式}{=}&\left[\int 4x^3dx\right]^2_0\\
=&\left[x^4\right]^2_0\qquad(積分定数は不要!)\\
=&2^4-0^4=16
\end{align}$$
(慣れたら2行目の式は省略して計算しよう.)
(2)
$$\begin{align}
&\int^1_{-1}(3x^2-x+1)dx\\
\underset{基本公式}{=}&\left[\int(3x^2-x+1)dx\right]^1_{-1}\\
=&\left[x^3-\dfrac{1}{2}x^2+x\right]^1_{-1}\qquad(積分定数は不要!)\\
=&\left(1^3-\dfrac{1}{2}\cdot 1^2+1\right)-\left((-1)^3-\dfrac{1}{2}\cdot(-1)^2+(-1)\right)\\
=&4
\end{align}$$
(慣れたら2行目の式は省略して計算しよう.)
