色々な関数を多項式で近似することや,
無限の多項式で表すことを学ぶ(教科書p107-109,149-152,195-198).
- $n$回微分
定義
関数$f(x)$を$n$回続けて微分することで得られる関数
$$\overbrace{\dfrac{d}{dx}\dfrac{d}{dx}\cdots\dfrac{d}{dx}}^{n個}f(x)$$
を
$f(x)$のn回微分, 又は, n次導関数といい,
$$f^{(n)},\quad f^{(n)}(x),\quad \dfrac{d^nf}{dx^n},\quad \dfrac{d^n}{dx^n}f(x)$$
などで表す.
- 例題
- p96例1
(1) $(x^4+2x^3-3x^2+5x-3)^{\prime\prime}=?$
(2) $(x^2e^x)^{\prime\prime}=?$
答.
(1)
$$(x^4+2x^3-3x^2+5x-3)^{\prime\prime}=(4x^3+6x^2-6x+5)^\prime=12x^2+12x-6$$
(2)
$$(x^2e^x)^{\prime\prime}=((x^2+2x)e^x)^\prime=(x^2+4x+2)e^x$$
- p108の例1
$$(e^x)^\prime=e^x$$
$$(e^x)^{\prime\prime}=(e^x)^\prime=e^x$$
$$......$$
$$(e^x)^{(n)}=e^x$$
- p108の例2
$$(\sin x)^\prime=\cos x$$
$$(\sin x)^{\prime\prime}=(\cos x)^\prime=-\sin x$$
$$(\sin x)^{\prime\prime\prime}=(-\sin x)^\prime=-\cos x$$
$$(\sin x)^{\prime\prime\prime\prime}=(-\cos x)^\prime=\sin x$$
$$(\sin x)^{(5)}=(\sin x)^\prime=\cos x$$
$$......$$
- 高次導関数の役割
高次導関数を考えると次の点で役立つ.
1. 関数の増減や凸凹の具合を把握し, グラフの概形を調べる.
2. 関数を多項式で近似する.
以下では, 上の2に関して学んでいく.
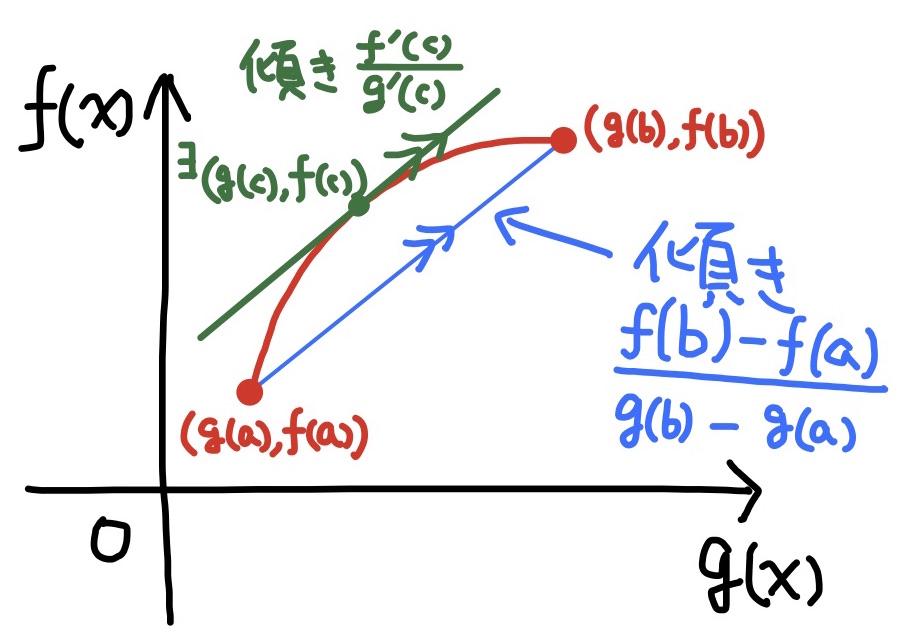
- コーシーの平均値の定理(微分の復習)
定理(p200)
$a<b$とする.
微分可能関数$f(x),g(x)$について
$$\dfrac{f(b)-f(a)}{g(b)-g(a)}=\dfrac{f^\prime(c)}{g^\prime(c)}\qquad(a<{}^\exists c<b)$$
が成り立つ.
但し$g^\prime(x)\ne 0$ ($a<x<b$), $g(b)\ne g(a)$とする.
- 積分版のコーシーの平均値の定理
定理
$a<b$とする.
積分可能関数$f(x),g(x)$について
$$\dfrac{\int^b_af(x)dx}{\int^b_ag(x)dx}=\dfrac{f(c)}{g(c)}\qquad(a<{}^\exists c<b)$$
が成り立つ.
但し$g(x), \displaystyle\int^b_a g(x)\ne 0$ ($a<x<b$)とする.
証明.
コーシーの平均値の定理を書き換えると,
$$\begin{align}
\underset{コーシーの定理}{\Longrightarrow}&\dfrac{f(b)-f(a)}{g(b)-g(a)}=\dfrac{f^\prime(c)}{g^\prime(c)}\qquad(a<{}^\exists c<b)\\
\underset{変形}{\Longrightarrow}&\dfrac{\Big[f(x)\Big]^b_a}{\Big[g(x)\Big]^b_a}=\left.\dfrac{f^\prime(x)}{g^\prime(x)}\right|_{x=c}\qquad(a<{}^\exists c<b)\\
\underset{f,gに\int fdx,\int gdxを代入}{\Longrightarrow}&
\dfrac{\Big[\int f(x)dx\Big]^b_a}{\Big[\int g(x)dx\Big]^b_a}=\left.\dfrac{\dfrac{d}{dx}\int f(x)dx}{\dfrac{d}{dx}\int g(x)dx}\right|_{x=c}\qquad(a<{}^\exists c<b)\\
\underset{基本定理と約分より}{\Longrightarrow}&
\dfrac{\int^b_a f(x)dx}{\int^b_a g(x)dx}=\left.\dfrac{f(x)}{g(x)}\right|_{x=c}\qquad(a<{}^\exists c<b)\\
\underset{右辺で代入}{\Longrightarrow}&
\dfrac{\int^b_a f(x)dx}{\int^b_a g(x)dx}=\dfrac{f(c)}{g(c)}\qquad(a<{}^\exists c<b)\\
\end{align}$$
系
$$\int^b_af(x)g(x)dx=f(c)\int^b_ag(x)dx\qquad(a<{}^\exists c<b)$$
証明.
$$\begin{align}
\underset{積分版コーシーの平均値の定理}{\Longrightarrow}&\dfrac{\int^b_af(x)dx}{\int^b_ag(x)dx}=\dfrac{f(c)}{g(c)}\qquad(a<{}^\exists c<b)\\
\underset{f(x)にf(x)g(x)を代入}{\Longrightarrow}&\dfrac{\int^b_af(x)g(x)dx}{\int^b_ag(x)dx}=\dfrac{f(c)g(c)}{g(c)}\qquad(a<{}^\exists c<b)\\
\underset{等式変形}{\Longrightarrow}&\int^b_af(x)g(x)dx=f(c)\int^b_ag(x)dx\qquad(a<{}^\exists c<b)\\
\end{align}$$
- 今回の要点
1. 何回か微分して得られる関数を高次導関数という.
2. 高次導関数は関数の多項式近似に役立つ.
3. $\displaystyle\int^b_af(x)g(x)dx=f(c)\int^b_ag(x)dx\qquad(a<{}^\exists c<b)$
(次回使う.)
- 課題
p111-112のA,Bの中から4問以上解きなさい.
- 部分積分(復習)
$$\int^b_a f(t)G^\prime(t)dx=\Big[f(t)G(t)\Big]^b_a-\int^b_af^\prime(t)G(t)dt$$
- 部分積分による関数の変形
関数$f(x)$は何回でも微分可能であるとする.
$$f(b)-f(a)\underset{基本公式}{=}\int^b_af^\prime(t)dt$$
である. よって, 式変形して
$$f(b)=f(a)+\int^b_af^\prime(t)dt$$
を得る.
右辺で部分積分を繰り返し適用してみる.
$$\begin{align}
f(b)&=f(a)+\int^b_af^\prime(t)dt\\
&=f(a)-\int^b_af^\prime(t)(b-t)^\prime dt\\
&\underset{部分積分}{=}f(a)-\Big[f^\prime(t)(b-t)\Big]^b_a+\int^b_af^{\prime\prime}(t)(b-t) dt\\
&=f(a)+f^\prime(a)(b-a)+\int^b_af^{\prime\prime}(t)(b-t) dt\\
&=f(a)+f^\prime(a)(b-a)-\int^b_af^{\prime\prime}(t)\left(\dfrac{(b-t)^2}{2}\right)^\prime dt\\
&\underset{部分積分}{=}f(a)+f^\prime(a)(b-a)-\left[f^{\prime\prime}(t)\left(\dfrac{(b-t)^2}{2}\right)\right]^b_a+\int^b_af^{(3)}(t)\left(\dfrac{(b-t)^2}{2}\right)dt\\
&=f(a)+f^\prime(a)(b-a)+f^{\prime\prime}(a)\cdot \dfrac{(b-a)^2}{2}+\int^b_af^{(3)}(t)\left(\dfrac{(b-t)^2}{2}\right)dt\\
&=f(a)+f^\prime(a)(b-a)+f^{\prime\prime}(a)\cdot \dfrac{(b-a)^2}{2}-\int^b_af^{(3)}(t)\left(\dfrac{(b-t)^3}{3!}\right)^\prime dt\\
&\underset{部分積分}{=}f(a)+f^\prime(a)(b-a)+f^{\prime\prime}(a)\cdot \dfrac{(b-a)^2}{2}-\int^b_af^{(3)}(t)\left(\dfrac{(b-t)^3}{3!}\right)^\prime dt\\
&\underset{同様の計算をして}{=}f(a)+f^\prime(a)(b-a)+f^{\prime\prime}(a)\cdot \dfrac{(b-a)^2}{2}+f^{(3)}(a)\cdot\dfrac{(b-a)^3}{3!}+\int^b_af^{(4)}(t)\left(\dfrac{(b-t)^3}{3!}\right) dt\\
&=......\\
&=f(a)+\dfrac{f^\prime(a)}{1!}(b-a)+\dfrac{f^{(2)}(a)}{2!}(b-a)^2+\cdots+\dfrac{f^{(n)}(a)}{n!}(b-a)^n+\int^b_a\dfrac{f^{(n+1)}(t)}{n!}(b-t)^ndt\\
\end{align}$$
よって等式
$$f(b)=多項式項\sum^{n}_{k=0}\dfrac{f^{(k)}(a)}{k!}(b-a)^k+積分項\int^b_a\dfrac{f^{(n+1)}(t)}{n!}(b-t)^ndt$$
が得られた.
さらに, 前回学んだ定理
$$\int^b_af(x)g(x)dx=f(c)\int^b_ag(x)dx\qquad(a<{}^\exists c<b)$$
を用いて積分項を変形すると,
$$\begin{align}
&積分項\int^b_a\dfrac{f^{(n+1)}(t)}{n!}(b-t)^ndt\\
&\underset{前回の定理}{=}\dfrac{f^{(n+1)}(c)}{n!}\int^b_a(b-t)^ndt\quad(a<{}^\exists c<b)\\
&\underset{積分計算}{=}\dfrac{f^{(n+1)}(c)}{(n+1)!}\left[-\dfrac{(b-t)^{n+1}}{n+1}\right]^b_a\quad(a<{}^\exists c<b)\\
&\underset{積分計算}{=}\dfrac{f^{(n+1)}(c)}{(n+1)!}(b-a)^{n+1}\quad(a<{}^\exists c<b)\\
\end{align}$$
従って, 等式
$$f(b)=多項式項\sum^{n}_{k=0}\dfrac{f^{(k)}(a)}{k!}(b-a)^k+剰余項\dfrac{f^{(n+1)}(c)}{(n+1)!}(b-a)^{n+1}\quad(a<{}^\exists c<b)$$
が得られた.
$b$に変数$x$を代入したものをテイラーの定理という.
定理
何回でも微分可能な関数$f(x)$は
$$f(x)=多項式項\sum^{n}_{k=0}\dfrac{f^{(k)}(a)}{k!}(x-a)^k+剰余項\dfrac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}$$
と変形できる. (ただし, $c$は$a$と$x$の間の数)
- テイラー展開(p198)
テイラーの定理において, $n\to\infty$としてみる.
もしも
$$剰余項\dfrac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}\to 0\qquad(n\to\infty)\tag{*}$$
であれば,
関数$f(x)$は無限の多項式によって,
$$\begin{align}
f(x)&=\sum^\infty_{k=0}\dfrac{f^{(k)}(a)}{k!}(x-a)^k\\
&=f(a)+\dfrac{f^\prime(a)}{1!}(x-a)+\dfrac{f^{\prime\prime}(a)}{2!}(x-a)^2+\cdots
+\dfrac{f^{(n)}(a)}{n!}(x-a)^n+\cdots
\end{align}$$
と表される.
この右辺を$f(x)$のテイラー展開といい, $x=a$をこの展開の中心という.
- マクローリン展開(p196)
中心$0$のテイラー展開
$$\begin{align}
f(x)&=\sum^\infty_{k=0}\dfrac{f^{(k)}(0)}{k!}x^k\\
&=f(0)+\dfrac{f^\prime(0)}{1!}x+\dfrac{f^{\prime\prime}(0)}{2!}x^2+\cdots
+\dfrac{f^{(n)}(0)}{n!}x^n+\cdots
\end{align}$$
を$f(x)$のマクローリン展開という.
- p196例題1
以下の関数のマクローリン展開を求めなさい.
(1) $e^x$
(2) $\sin x$
(3) $\cos x$
答.
(1)
$$(e^x)^{(n)}=e^x$$
$$\left.(e^x)^{(n)}\right|_{x=0}=1$$
より,
$$\begin{align}
e^x&=\sum^\infty_{n=0}\dfrac{1}{n!}x^n\\
&=1+\dfrac{1}{1!}x+\dfrac{1}{2!}x^2+\cdots
+\dfrac{1}{n!}x^n+\cdots
\end{align}$$
(2)
$$(\sin x)^{(2n)}=(-1)^n\sin x\qquad(\sin x)^{(2n+1)}=(-1)^n\cos x$$
$$\left.(\sin x)^{(2n)}\right|_{x=0}=0\qquad \left.(\sin x)^{(2n+1)}\right|_{x=0}=(-1)^{n}$$
より,
$$\begin{align}
\sin x&=\sum^\infty_{n=0}\dfrac{(-1)^n}{(2n+1)!}x^{2n+1}\\
&=\dfrac{1}{1!}x-\dfrac{1}{3!}x^3+\dfrac{1}{5!}x^5-\cdots
+\dfrac{(-1)^n}{(2n+1)!}x^{2n+1}+\cdots
\end{align}$$
(3)
$$(\cos x)^{(2n)}=(-1)^n\cos x\qquad(\cos x)^{(2n+1)}=(-1)^{n+1}\sin x$$
$$\left.(\cos x)^{(2n)}\right|_{x=0}=(-1)^n\qquad \left.(\cos x)^{(2n+1)}\right|_{x=0}=0$$
より,
$$\begin{align}
\cos x&=\sum^\infty_{n=0}\dfrac{(-1)^{n}}{(2n)!}x^{2n}\\
&=1-\dfrac{1}{2!}x^2+\dfrac{1}{4!}x^4-\cdots
+\dfrac{(-1)^n}{(2n)!}x^{2n}+\cdots
\end{align}$$
- 今回の要点
1. テイラー展開
$$\begin{align}
f(x)&=\sum^\infty_{n=0}\dfrac{f^{(n)}(a)}{n!}(x-a)^n\\
&=f(a)+\dfrac{f^\prime(a)}{1!}(x-a)+\dfrac{f^{\prime\prime}(a)}{2!}(x-a)^2+\cdots
+\dfrac{f^{(n)}(a)}{n!}(x-a)^n+\cdots
\end{align}$$
2. マクローリン展開
$$\begin{align}
f(x)&=\sum^\infty_{n=0}\dfrac{f^{(n)}(0)}{n!}x^n\\
&=f(0)+\dfrac{f^\prime(0)}{1!}x+\dfrac{f^{\prime\prime}(0)}{2!}x^2+\cdots
+\dfrac{f^{(n)}(0)}{n!}x^n+\cdots
\end{align}$$
3. テイラー展開やマクローリン展開ができるためには,
$$剰余項\dfrac{f^{(n+1)}(c)}{(n+1)!}(x-a)^{n+1}\to 0\qquad(n\to\infty)\tag{*}$$
でなければならない.
- 課題
p198-199のA3-4,B1-4の中から2問以上解きなさい.

